giải phương trình :x^2 +(10/x) ^2 =25
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Sorry đề là: √(25-x^2)-√(10-x^2)=3
mà mình làm đc rùi. Dù sao cũng cảm ơn các bạn :D
=> √(25-x^2)=3+√(10-x^2)
bình phương 2 vế
=> 25-x^2=9+10-x^2+6√(10-x^2)
<=> 6 = 6√(10-x^2)
<=> 1 = √(10-x^2)
bình phương típ 2 vế
=> 10-x^2 = 1
<=> x^2 = 9
=> x = +3 hoặc -3

\(\dfrac{x^2-26}{10}+\dfrac{x^2-25}{11}\ge\dfrac{x^2-24}{12}+\dfrac{x^2-23}{13}\)
\(\Leftrightarrow\left(\dfrac{x^2-26}{10}-1\right)+\left(\dfrac{x^2-25}{11}-1\right)\ge\left(\dfrac{x^2-24}{12}-1\right)+\left(\dfrac{x^2-23}{13}-1\right)\)
\(\Leftrightarrow\dfrac{x^2-36}{10}+\dfrac{x^2-36}{11}\ge\dfrac{x^2-36}{12}+\dfrac{x^2-36}{13}\)
\(\Leftrightarrow\dfrac{x^2-36}{10}+\dfrac{x^2-36}{11}-\dfrac{x^2-36}{12}-\dfrac{x^2-36}{13}\ge0\)
\(\Leftrightarrow\left(x^2-36\right)\left(\dfrac{1}{10}+\dfrac{1}{11}-\dfrac{1}{12}-\dfrac{1}{13}\right)\ge0\)
Vì \(\dfrac{1}{10}+\dfrac{1}{11}-\dfrac{1}{12}-\dfrac{1}{13}>0\Rightarrow x^2-36\ge0\Leftrightarrow\left[{}\begin{matrix}x\le-6\\x\ge6\end{matrix}\right.\)
Bất phương trình đó tương đương với:
\(\left(\dfrac{x^2-26}{10}-1\right)+\left(\dfrac{x^2-25}{11}-1\right)\ge\left(\dfrac{x^2-24}{12}-1\right)+\left(\dfrac{x^2-23}{13}-1\right)\)
⇔ \(\dfrac{x^2-36}{10}+\dfrac{x^2-36}{11}\ge\dfrac{x^2-36}{12}+\dfrac{x^2-36}{13}\)
⇔ \(\dfrac{x^2-36}{10}+\dfrac{x^2-36}{11}-\dfrac{x^2-36}{12}-\dfrac{x^2-36}{13}\ge0\)
⇔ \(\left(x^2-36\right)\left(\dfrac{1}{10}+\dfrac{1}{11}-\dfrac{1}{12}-\dfrac{1}{13}\right)\ge0\)
+)Vì \(\dfrac{1}{10}>\dfrac{1}{11}>\dfrac{1}{12}>\dfrac{1}{13}\) nên \(\dfrac{1}{10}+\dfrac{1}{11}-\dfrac{1}{12}-\dfrac{1}{13}>0\)
⇔ \(x^2-36\ge0\)
⇔ \(x^2\ge36\)
⇔ \(\sqrt{x^2}\ge6\)
⇔ \(\left|x\right|\ge6\)
⇔ \(\left[{}\begin{matrix}x\ge6\\x\le-6\end{matrix}\right.\)
➤ Vậy \(\left[{}\begin{matrix}x\ge6\\x\le-6\end{matrix}\right.\)


a: (2x-10)(5x+25)=0
=>2x-10=0 hoặc 5x+25=0
=>x=5 hoặc x=-5
b: (x+15)(x-2)=0
=>x+15=0 hoặc x-2=0
=>x=-15 hoặc x=2
c: =>x(x-7)=0
=>x=0 hoặc x=7

\(\left\{{}\begin{matrix}x^2+y^2=25\\x.y=10\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x^2+y^2=25\\x=\dfrac{10}{y}\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}\left(\dfrac{10}{y}\right)^2+y^2=25\\x=\dfrac{10}{y}\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}\dfrac{100}{y^2}+y^2=25\\x=\dfrac{10}{y}\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}100+y^4-25y^2=0\\x=\dfrac{10}{y}\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}y^2=20\\y^2=5\end{matrix}\right.\\x=\dfrac{10}{y}\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}y=\pm\sqrt{20}\\y=\pm\sqrt{5}\end{matrix}\right.\\x=\dfrac{10}{y}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}y=\sqrt{20};x=\sqrt{5}\\y=-\sqrt{20};x=-\sqrt{5}\\y=-\sqrt{5};x=-\sqrt{20}\\y=\sqrt{5};x=\sqrt{20}\end{matrix}\right.\)

\(DK:x\in\left[-\sqrt{10};\sqrt{10}\right]\)
PT\(\Leftrightarrow\left(\sqrt{25-x^2}-4\right)+\left(1-\sqrt{10-x^2}\right)=0\)
\(\Leftrightarrow\frac{9-x^2}{\sqrt{25-x^2}+4}-\frac{9-x^2}{1+\sqrt{10-x^2}}=0\)
\(\Leftrightarrow\left(9-x^2\right)\left(\frac{1}{\sqrt{25-x^2}+4}-\frac{1}{1+\sqrt{10-x^2}}\right)=0\)
Ta di chung minh:
\(\sqrt{25-x^2}+4>1+\sqrt{10-x^2}\)
\(\Leftrightarrow41-x^2+8\sqrt{25-x^2}>11-x^2+2\sqrt{10-x^2}\)
\(\Leftrightarrow15+4\sqrt{25-x^2}>\sqrt{10-x^2}\)
\(\Leftrightarrow325-x^2+120\sqrt{25-x^2}>10-x^2\)
\(\Leftrightarrow315+120\sqrt{25-x^2}>0\left(True\right)\)
\(\Rightarrow\frac{1}{\sqrt{25-x^2}+4}-\frac{1}{1+\sqrt{10-x^2}}< 0\)
\(\Rightarrow\orbr{\begin{cases}x=3\left(n\right)\\x=-3\left(n\right)\end{cases}}\)
Vay PT co nghiem la \(x=3\)va \(x=-3\)

\(a,2x-5=-x+4\\ \Leftrightarrow3x=9\\ \Leftrightarrow x=3\\ b,\left(4x-10\right)\left(25+5x\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}4x-10=0\\25+5x=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=-5\end{matrix}\right.\\ c,\dfrac{x}{3}-\dfrac{2x+1}{2}=\dfrac{x}{6}-x\\ \Leftrightarrow\dfrac{2x}{6}-\dfrac{3\left(2x+1\right)}{6}-\dfrac{x}{6}+\dfrac{6x}{6}=0\\ \Leftrightarrow2x-6x-3-x+6x=0\\ \Leftrightarrow x-3=0\\ \Leftrightarrow x=3\)
d, ĐKXĐ:\(x\ne-2,x\ne3\)
\(1+\dfrac{x}{3-x}=\dfrac{5x}{\left(x+2\right)\left(3-x\right)}+\dfrac{2}{x+2}\\ \Leftrightarrow\dfrac{\left(x+2\right)\left(3-x\right)}{\left(x+2\right)\left(3-x\right)}+\dfrac{x\left(x+2\right)}{\left(x+2\right)\left(3-x\right)}-\dfrac{5x}{\left(x+2\right)\left(3-x\right)}-\dfrac{2\left(3-x\right)}{\left(x+2\right)\left(3-x\right)}=0\\ \Leftrightarrow\dfrac{-x^2+x+6}{\left(x+2\right)\left(3-x\right)}+\dfrac{x^2+2x}{\left(x+2\right)\left(3-x\right)}-\dfrac{5x}{\left(x+2\right)\left(3-x\right)}-\dfrac{6-2x}{\left(x+2\right)\left(3-x\right)}=0\)
\(\Leftrightarrow\dfrac{-x^2+x+6+x^2+2x-5x-6+2x}{\left(x+2\right)\left(3-x\right)}=0\\ \Rightarrow0=0\left(luôn.đúng\right)\)

a) Xét tam thức \(f\left( x \right) = 7{x^2} - 19x - 6\) có \(\Delta = 529 > 0\), có hai nghiệm phân biệt \({x_1} = - \frac{2}{7},{x_2} = 3\) và có \(a = 7 > 0\)
Ta có bảng xét dấu như sau

Vậy nghiệm của bất phương trình là đoạn \(\left[ { - \frac{2}{7};3} \right]\)
b) \( - 6{x^2} + 11x > 10 \Leftrightarrow - 6{x^2} + 11x - 10 > 0\)
Xét tam thức \(f\left( x \right) = - 6{x^2} + 11x - 10\) có \(\Delta = - 119 < 0\)và có \(a = - 6 < 0\)
Ta có bảng xét dấu như sau

Vậy bất phương trình vô nghiệm
c) \(3{x^2} - 4x + 7 > {x^2} + 2x + 1 \Leftrightarrow 2{x^2} - 6x + 6 > 0\)
Xét tam thức \(f\left( x \right) = 2{x^2} - 6x + 6\) có \(\Delta = - 12 < 0\)và có \(a = 2 > 0\)
Ta có bảng xét dấu như sau
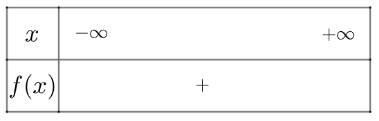
Vậy bất phương trình có vô số nghiệm
d) Xét tam thức \(f\left( x \right) = {x^2} - 10x + 25\) có \(\Delta = 0\), có nghiệm kép \({x_1} = {x_2} = 5\) và có \(a = 1 > 0\)
Ta có bảng xét dấu như sau

Vậy nghiệm của bất phương trình là \(x = 5\)

a) Sai lầm là coi -2 là hạng từ và chuyển vế hạng tử này trong khi -2 là một nhân tử.
Lời giải đúng:
-2x > 23
⇔ x < 23 : (-2) (chia cho số âm nên đổi chiều)
⇔ x < -11,5
Vậy nghiệm của bất phương trình là x < -11,5
b) Sai lầm là nhân hai vế của bất phương trình với 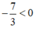 mà không đổi chiều bất phương trình.
mà không đổi chiều bất phương trình.
Lời giải đúng:
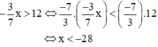
Vậy nghiệm của bất phương trình là x < -28

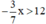 . Ta có:
. Ta có: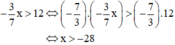
X²+(10/2)²=25
X= khác 2√5
X=-√5
X=√5