có vẽ hình ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NH
vẽ hình giúp e ạ có gì giải ra ạ em cảm ơn ạ=))
1
25 tháng 10 2023
10: Chọn B
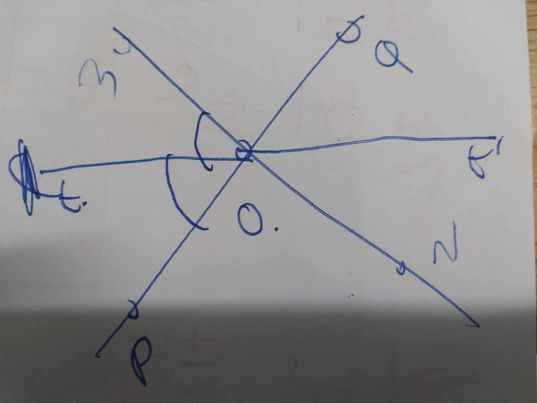
Ot là phân giác của \(\widehat{MOP}\)
=>\(\widehat{MOP}=2\cdot\widehat{tOP}\)
\(\widehat{MOP}=\widehat{NOQ}\)
=>\(\widehat{NOQ}=2\cdot\widehat{tOP}\)
mà \(\widehat{tOP}=\widehat{t'OQ}\)(hai góc đối đỉnh)
nên \(\widehat{NOQ}=2\cdot\widehat{t'OQ}\)
=>Ot' là phân giác của góc NOQ
11:
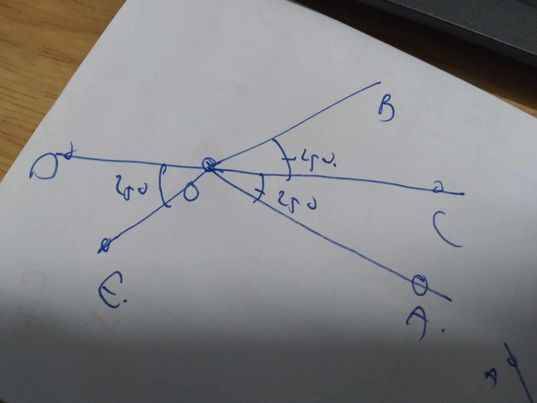
OC là phân giác của góc AOB
=>\(\widehat{AOC}=\widehat{BOC}=\dfrac{50^0}{2}=25^0\)
\(\widehat{DOE}=\widehat{BOC}\left(=25^0\right)\)
=>\(\widehat{DOE}+\widehat{DOB}=180^0\)
=>OB và OE là hai tia đối nhau
=>Hai góc đối đỉnh là \(\widehat{BOC};\widehat{DOE}\)
=>Chọn D
12:
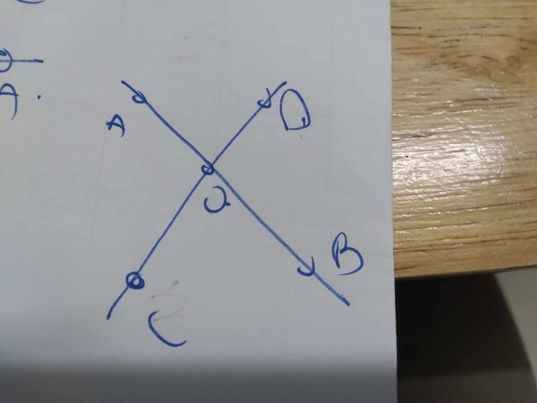
\(\widehat{AOC}+\widehat{AOD}=180^0\)
\(\widehat{AOC}-\widehat{AOD}=50^0\)
Do đó: \(\widehat{AOC}=\dfrac{180^0+50^0}{2}=115^0;\widehat{AOD}=115^0-50^0=65^0\)
=>\(\widehat{BOC}=\widehat{AOD}=65^0\)
=>Chọn B
31 tháng 12 2023
a: Xét (O) có
ΔAKB nội tiếp
AB là đường kính
Do đó: ΔAKB vuông tại K
Xét tứ giác EMBK có \(\widehat{EMB}+\widehat{EKB}=90^0+90^0=180^0\)
nên EMBK là tứ giác nội tiếp
b: Xét (O) có
OA là bán kính
OA\(\perp\)CD tại M
Do đó: \(sđ\stackrel\frown{AC}=sđ\stackrel\frown{AD}\)
Xét (O) có
\(\widehat{AKC}\) là góc nội tiếp chắn cung AC
\(\widehat{ACD}\) là góc nội tiếp chắn cung AD
\(sđ\stackrel\frown{AD}=sđ\stackrel\frown{AC}\)
Do đó: \(\widehat{AKC}=\widehat{ACD}\)
Xét ΔAKC và ΔACE có
\(\widehat{AKC}=\widehat{ACE}\)
\(\widehat{KAC}\) chung
Do đó: ΔAKC đồng dạng với ΔACE
=>\(\dfrac{AK}{AC}=\dfrac{AC}{AE}\)
=>\(AE\cdot AK=AC^2\)
có vẽ hình lun ạ
31 tháng 12 2023
1:
Ta có: ΔABC vuông tại C
mà ΔCAB nội tiếp (O)
nên O là trung điểm của AB
Xét tứ giác OBDC có \(\widehat{OBD}+\widehat{OCD}=90^0+90^0=180^0\)
nên OBDC là tứ giác nội tiếp
=>O,B,D,C cùng thuộc một đường tròn
Xét (O) có
DC,DB là các tiếp tuyến
Do đó: DC=DB
=>D nằm trên đường trung trực của CB(1)
Ta có: OC=OB
=>O nằm trên đường trung trực của CB(2)
Từ (1) và (2) suy ra OD là đường trung trực của CB
=>OD\(\perp\)CB
Ta có: AC\(\perp\)CB
CB\(\perp\)OD
Do đó: OD//AC
2: Xét (O) có
ΔBEA nội tiếp
AB là đường kính
Do đó: ΔBAE vuông tại E
=>BE\(\perp\)EA tại E
=>BE\(\perp\)AD tại E
Xét ΔBAD vuông tại B có BE là đường cao
nên \(DE\cdot DA=DB^2\left(3\right)\)
Xét ΔDOB vuông tại B có BH là đường cao
nên \(DH\cdot DO=DB^2\)(4)
Từ (3) và (4) suy ra \(DE\cdot DA=DH\cdot DO\)
25 tháng 8 2023
a: Xét ΔOCD có OC=OD và \(\widehat{COD}=90^0\)
nên ΔOCD vuông cân tại O
b: \(\widehat{COD}=90^0\)
=>sđ cung nhỏ CD=90 độ
sđ cung lớn CD là: 360-90=270 độ
ΔOCD vuông tại O
=>\(CD^2=OC^2+OD^2=2R^2\)
=>\(CD=R\sqrt{2}\)
25 tháng 8 2023
a: Xét ΔOMN có OM=ON và góc MON=60 độ
nên ΔOMN đều
b: góc MON=60 độ
=>sđ cung nhỏ MN=60 độ
sđ cung lớn MN là:
360-60=300 độ
25 tháng 8 2023
a: \(sđ\stackrel\frown{AmB}=60^0\)
=>\(\widehat{AOB}=60^0\)
\(sđ\stackrel\frown{AnB}=360^0-60^0=300^0\)
b: Xét ΔOAB có OA=OB và góc AOB=60 độ
nên ΔOAB đều
=>AB=OA=R
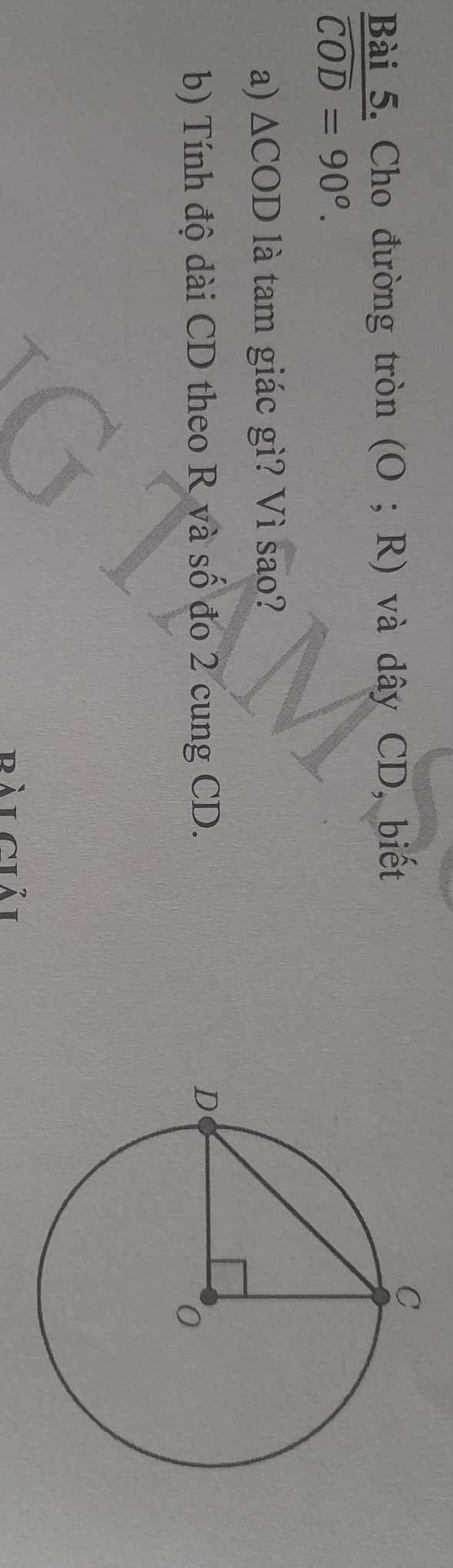
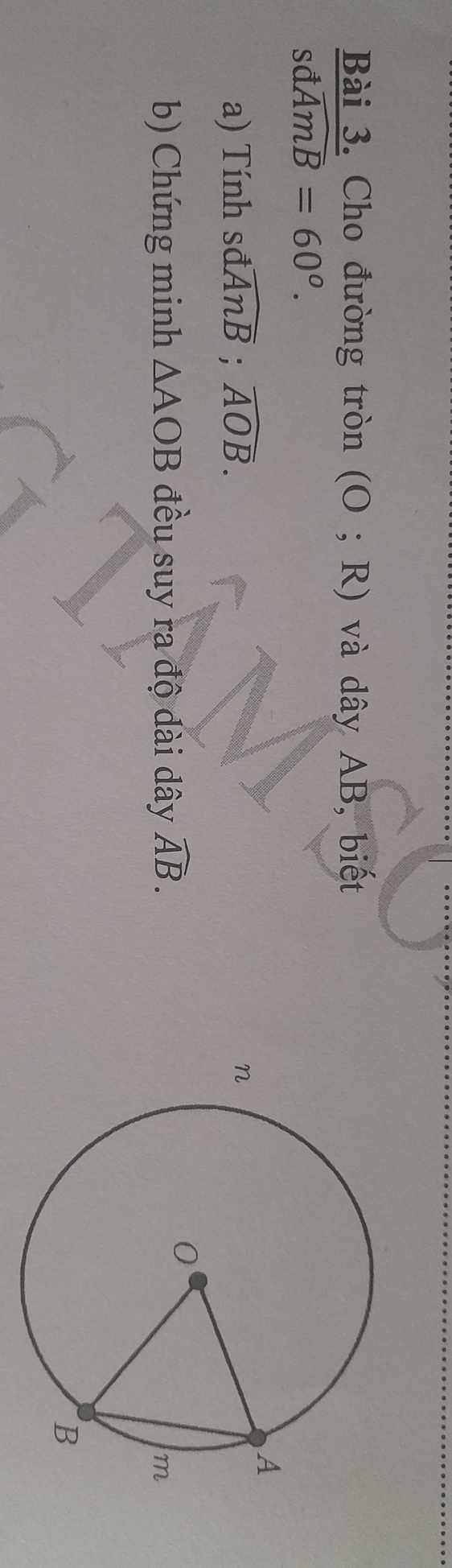
a: Ta có: ΔCAB cân tại C
=>\(\widehat{CAB}=\widehat{CBA}\)
mà \(\widehat{CBA}=50^0\)
nên \(\widehat{CAB}=50^0\)
Ta có: ΔCAB cân tại C
=>\(\widehat{ACB}=180^0-2\cdot\widehat{CAB}=80^0\)
Xét ΔCAB có \(\widehat{ACB}>\widehat{CAB}=\widehat{CBA}\)
mà AB,CB,CA lần lượt là cạnh đối diện của các góc ACB,CAB,CBA
nên AB>CB=CA
b: Xét ΔCIA vuông tại I và ΔCIB vuông tại I có
CA=CB
CI chung
Do đó: ΔCIA=ΔCIB
=>IA=IB
c: Ta có: ΔCIA=ΔCIB
=>\(\widehat{ACI}=\widehat{BCI}\)
Xét ΔCHI vuông tại H và ΔCKI vuông tại K có
CI chung
\(\widehat{HCI}=\widehat{KCI}\)
Do đó: ΔCHI=ΔCKI
=>IH=IK
d: Ta có: ΔCHI=ΔCKI
=>CH=CK
=>ΔCHK cân tại C