cho A nằm ngoài O kẻ hai tiếp tuyến AB và AC (B,C là tiếp điểm ) Chứng tỏ tứ giác ABC nội tiếp đường tròn Xác định tâm đường tròn ngoại tiếp tứ giác ABOC
b) vẽ dây BE song song với AC Gọi D là giao điểm thứ hai của AE với (O) DB cắt AC tại K
+CM : KA^2=KB.KD
+K là trung điểm AC
c) AE cắt BC tại H,KH cắt BE tại M.chứng minh OM vuông góc với BE
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1) Ta có \(\widehat{ABO}=\widehat{ACO}=90độ\left(gt\right)\)
Do đó\(\widehat{ABO}+\widehat{ACO}=180độ\)
Nên tứ giác ABOC nội tiếp đường tròn đường kính AO
Tâm đường tròn ngoại tiếp tứ giác ABOC là trung điểm AO.
2) Xét ΔABD và ΔAEB có
\(\widehat{BAE}\)chung
\(\widehat{ABD}=\widehat{AEB}\)(góc tạo bởi tia tiếp tuyến và dây và góc nội tiếp cùng chắn \(\widebat{BD}\))
Nên ΔABD 
Do đó \(\frac{AB}{AE}\)=\(\frac{AD}{AB}\)
Hay AB2= AE.AD

1: góc ABO+góc ACO=180 độ
=>ABOC nội tiếp đường tròn đường kính OA
Tâm là trung điểm của OA
2: Xét ΔABE và ΔAFB có
góc ABE=góc AFB
góc BAE chung
=>ΔABE đồng dạng với ΔAFB
=>AB/AF=AE/AB
=>AB^2=AE*AF

a: góc OBA+góc OCA=180 độ
=>OBAC nội tiếp
b: Xét (O) có
AB,AC là tiếp tuyến
=>AB=AC
mà OB=OC
nên OA là trung trực của BC
=>AH*AO=AB^2
Xét ΔABD và ΔAEB có
góc ABD=góc AEB
góc BAD chung
=>ΔABD đồng dạng với ΔAEB
=>AB^2=AD*AE=AH*AO

a) Xét tứ giác ABOC có
\(\widehat{ABO}\) và \(\widehat{ACO}\) là hai góc đối
\(\widehat{ABO}+\widehat{ACO}=180^0\)
Do đó: ABOC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)

Lời giải 1 bài toán tương tự - Dài và khó
Giải toán: Bài hình trong đề thi HK2 Lớp 9 | Rất phức tạp. - YouTube

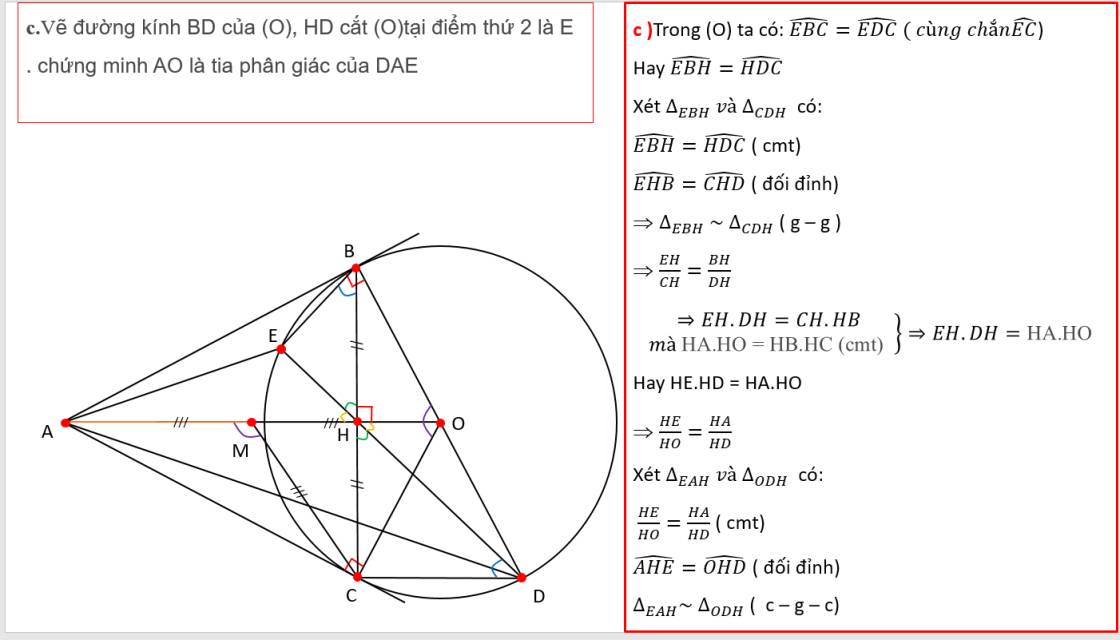

a: Xét tứ giác ABOC có \(\widehat{OBA}+\widehat{OCA}=90^0+90^0=180^0\)
nên ABOC là tứ giác nội tiếp đường tròn đường kính OA
tâm là trung điểm của OA
b: Xét (O) có
\(\widehat{ABD}\) là góc tạo bởi tiếp tuyến BA và dây cung BD
\(\widehat{BED}\) là góc nội tiếp chắn cung BD
Do đó: \(\widehat{ABD}=\widehat{BED}\)
mà \(\widehat{BED}=\widehat{DAK}\)(hai góc so le trong, BE//AC)
nên \(\widehat{KAD}=\widehat{KBA}\)
Xét ΔKAD và ΔKBA có
\(\widehat{KAD}=\widehat{KBA}\)
\(\widehat{AKD}\) chung
Do đó: ΔKAD~ΔKBA
=>\(\dfrac{KA}{KB}=\dfrac{KD}{KA}\)
=>\(KA^2=KB\cdot KD\)
Xét (O) có
\(\widehat{KCD}\) là góc tạo bởi tiếp tuyến CK và dây cung CD
\(\widehat{CBD}\) là góc nội tiếp chắn cung CD
Do đó: \(\widehat{KCD}=\widehat{CBD}\)
Xét ΔKCD và ΔKBC có
\(\widehat{KCD}=\widehat{KBC}\)
\(\widehat{CKD}\) chung
Do đó: ΔKCD~ΔKBC
=>\(\dfrac{KC}{KB}=\dfrac{KD}{KC}\)
=>\(KC^2=KB\cdot KD\)
=>KC=KA
=>K là trung điểm của AC