giá trị lớn nhất -X^2 -4x-y^2+2y
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(A=4x^2+y^2+xy+4x+2y+3=4x^2+x\left(y+4\right)+\frac{\left(y+4\right)^2}{16}+y^2-\frac{\left(y+4\right)^2}{16}+2y+3\)\(=\left(2x+\frac{y+4}{4}\right)^2+\frac{16y^2-y^2-8y-16+32y+48}{16}=\left(2x+\frac{y+4}{4}\right)^2+\frac{15y^2+24y+32}{16}\)\(=\left(2x+\frac{y+4}{4}\right)^2+\frac{15\left(y^2+\frac{24}{15}y+\frac{16}{25}\right)+\frac{112}{5}}{16}=\left(2x+\frac{y+4}{4}\right)^2+\frac{15\left(y+\frac{4}{5}\right)^2+\frac{112}{5}}{16}\ge\frac{\frac{112}{5}}{16}=\frac{7}{5}\)Đẳng thức xảy ra khi \(\hept{\begin{cases}2x+\frac{y+4}{4}=0\\y+\frac{4}{5}=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=-\frac{2}{5}\\y=-\frac{4}{5}\end{cases}}\)
\(B=-x^2-y^2-2xy=-\left(x+y\right)^2\le0\)
Đẳng thức xảy ra khi x = -y

Có x^2 + 2xy + 4x + 4y + 2y^2 + 3 = 0
--> (x+y)^2 + 4(x+y) + 4+ y^2 - 1 = 0
--> (x+y+2)^2 + y^2 = 1
-->(x+y+2)^2 <= 1 ( vì y^2 >=1)
--> -1 <= x+y+2 <=1
--> 2015 <= x+y+2018 <= 2017
hay 2015 <= Q , dau bang xay ra khi x+y+2=-1 --> x+y=-3
Q<=2017, dau bang xay ra khi x+y+2=1 --> x+y=-1
Vậy giá trị nhỏ nhất của Q là 2015 khi x+y =-3
giá trị lớn nhất của Q là 2017 khi x+y=-1

a)
\(A=4x-x^2+3=-\left(x^2-4x-3\right)=-\left(x^2-4x+4\right)+7=-\left(x-2\right)^2+7\le7\)
Daaus = xayr ra khi: x = 2
b) \(B=4x^2-12x+15=4\left(x^2-3x+9\right)-21=4\left(x-3\right)^2-21\ge-21\)
Dấu = xảy ra khi x = 3
c) \(C=4x^2+2y^2-4xy-4y+1=\left(4x^2-4xy+y^2\right)+\left(y^2-4y+4\right)-3=\left(2x-y\right)^2+\left(y-2\right)^2-3\ge-3\)
Dấu = xảy ra khi
2x = y và y = 2
=> x = 1 và y = 2
a) A = \(-x^2+4x+3=-\left(x-2\right)^2+7\le7\)
Dấu "=" <=> x = 2
b) \(4x^2-12x+15=\left(2x-3\right)^2+6\ge6\)
Dấu "=" xảy ra <=> \(x=\dfrac{3}{2}\)
c) \(4x^2+2y^2-4xy-4y+1\)
= \(\left(4x^2-4xy+y^2\right)+\left(y^2-4y+4\right)-3\)
= \(\left(2x-y\right)^2+\left(y-2\right)^2-3\ge-3\)
Dấu "=" <=> \(\left\{{}\begin{matrix}x=1\\y=2\end{matrix}\right.\)

\(a^2+b^2+6ab+2=2a+3b\Rightarrow\left(a+b\right)^2-3\left(a+b\right)+2=-a\left(4b+1\right)\le0\)
\(\Rightarrow\left(a+b-1\right)\left(a+b-2\right)\le0\Rightarrow1\le a+b\le2\)
\(a^2+b^2+6ab+2=2a+3b\Rightarrow4ab=-\left(a+b\right)^2+2a+3b-2\)
\(-P=\dfrac{6a+5b+4ab+7}{a+b+1}=\dfrac{6a+5a+7-\left(a+b\right)^2+2a+3b-2}{a+b+1}\)
\(=\dfrac{-\left(a+b\right)^2+8\left(a+b\right)+5}{a+b+1}\)
Tới đây có thể giải theo lớp 9 (tách thành tích hoặc bình phương) hoặc làm theo lớp 12 (khảo sát hàm \(f\left(x\right)=\dfrac{-x^2+8x+5}{x+1}\) trên \(\left[1;2\right]\)). Cả 2 việc đều dễ dàng cả
\(-P=6-\dfrac{\left(x-1\right)^2}{x+1}=\dfrac{17}{3}+\dfrac{\left(3x-1\right)\left(2-x\right)}{3\left(x+1\right)}\)


a) = 9(x2 - 2.x/2.9 + 1/324) - 9/324 +5
GTNN A = 4,97
b) = (2x +y)2 + y2 + 2018
GTNN B = 2018 khi x=0;y=0
c) = -4(x2 - 2.3x/ 4.2 + 9/16) +9/16 +10
GTLN C = 169/16
d) = -(x-y)2 - (2x +1) +1 + 2016
GTLN D = 2017
(trg bn cho bài khó dữ z, làm hại cả não tui)
II)tìm m để pt sau có ngiệm
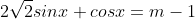

%5E2+1-(m-1)%5E2%5Cgeq0)

đk để có nghiệm là
theo pt trên ta có
<=>
(m=4 or m=-2)
=> m thuộc [-2;4]