Cho hình thang ABCD. Biết M,N lần lượt là trung điểm của hai đường chéo AC;BD. Chứng minh rằng MN // AC; BD. Chỉ dùng kiến thức lớp 8 (có thể dùng đường phần giác góc ngoài của tam giác)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NN
9 tháng 1 2019
a) Xét tam giác ABD có :
M là trung điểm của AB
F là trung điểm của BD
=) MF là đường trung bình của tam giác ABD
=) MF//AD và MF=\(\frac{1}{2}\)AD (1)
Xét tam giác tam giác ACD có :
N là trung điểm CD
E là trung điểm AC
=) NE là đường trung bình của tam giác ACD
=) NE//AD và NE=\(\frac{1}{2}\)AD (2)
Từ (1) và (2) =) Tứ giác MENF là hình bình hành
10 tháng 9 2021
a:Xét hình thang ABCD có
M là trung điểm của AD
MN//AB//CD
Do đó: N là trung điểm của BC
Xét ΔDAB có
M là trung điểm của AD
ME//AB
Do đó: E là trung điểm của BD
Xét ΔABC có
N là trung điểm của BC
NF//AB
Do đó: F là trung điểm của AC
24 tháng 10 2021
a: Xét hình thang ABCD có
M là trung điểm của AD
MN//AB//CD
Do đó: N là trung điểm của BC
Xét ΔADC có
M là trung điểm của AD
MF//DC
Do đó: F là trung điểm của AC
Xét ΔBDC có
N là trung điểm của BC
NE//DC
Do đó: E là trung điểm của BD
CM
21 tháng 1 2019
a) Áp dụng tính chất đường trung bình của tam giác cho DABC và DDBC ta sẽ có:
MQ//PN//BC và MQ = PN = 0.5BC ÞMPNQ là hình bình hành.
b) Tương tự ta có QN//MP//AD và QN = MP = 0.5AD.
Nên để MPNQ là hình thoi thì MN ^ PQ khi đó MN ^ CD và trung trực hay trục đối xứng của AB và CD.
Þ hình thang ABCD là hình thang cân
24 tháng 10 2021
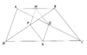
a: Xét ΔABC có
M là trung điểm của AB
P là trung điểm của AC
Do đó: MP là đường trung bình của ΔBAC
Suy ra: MP//BC và \(MP=\dfrac{BC}{2}\left(1\right)\)
Xét ΔBDC có
Q là trung điểm của BD
N là trung điểm của CD
Do đó: QN là đường trung bình của ΔBDC
Suy ra: QN//BC và \(QN=\dfrac{BC}{2}\left(2\right)\)
Từ (1) và (2) suy ra MP//QN và MP=QN
hay MQNP là hình bình hành
Gọi E là trung điểm của BC
∆ABC có:
E là trung điểm của BC
M là trung điểm của AC (gt)
⇒ EM là đường trung bình của ∆ABC
⇒ EM // AB (1)
∆BCD có:
E là trung điểm của BC
N là trung điểm của BD (gt)
⇒ EN là đường trung bình của ∆BCD
⇒ EN // CD (2)
Do ABCD là hình thang
⇒ AB // CD (3)
Từ (1), (2), (3) và theo tiên đề Ơclit ⇒ MN // AB // CD