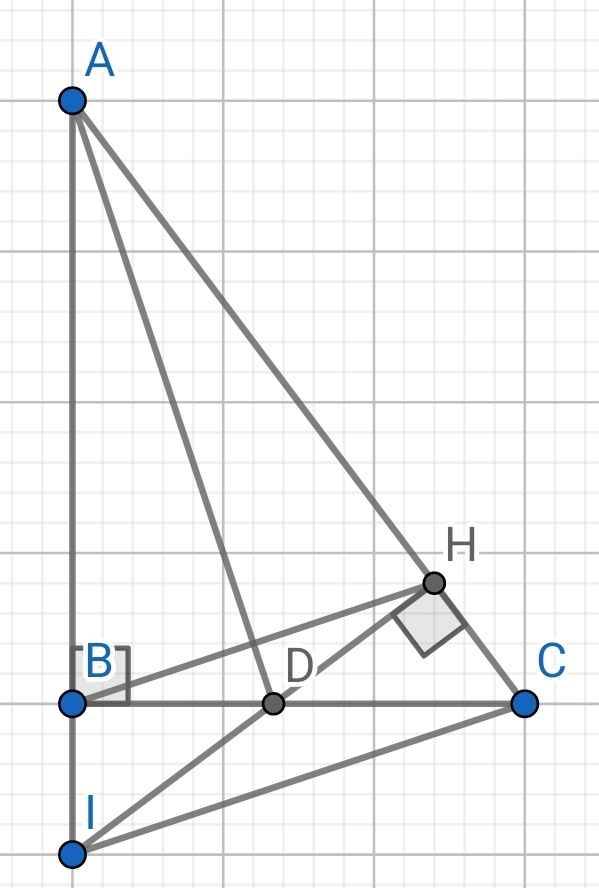
Cho tam giác ABC vuông tại B,p/g AD.Từ D,kẻ DH vuông góc AC(H thuộc AC).HD và AB kéo dài cắt nhau tại I.CMR:
a)Tam giác ABD=tam giác AHD
b)AD là trung trực
c)DIC cân
d)BH//IC
e)AD vuông góc với IC
f)BD<DC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
29 tháng 6 2019
Hình dễ tự vẽ nhé bạn
a ) Do \(DH\perp AC\Rightarrow\widehat{AHD}=90^o\)
Xét \(\Delta ABD\) và \(\Delta AHD\) có :
\(\widehat{BAD}=\widehat{HAD}\) ( AD là tia p/g )
AD là cạnh chung
\(\widehat{ABD}=\widehat{AHD}\left(=90^o\right)\)
nên \(\Delta ABD=\Delta AHD\left(g.c.g\right)\)
b ) Gọi K là giao điểm của BH và AD
Xét \(\Delta BAK\)và \(\Delta HAK\) có :
AB = AH ( do \(\Delta ABD=\Delta AHD\))
\(\widehat{BAK}=\widehat{HAK}\) ( AD là tia p/g )
AK là cạnh chung
nên \(\Delta BAK=\Delta HAK\left(c.g.c\right)\)
=> BK = HK ( 1 )
=> \(\widehat{AKB}+\widehat{AKH}=180^o\) ( hai góc kề bù )
\(\widehat{AKB}+\widehat{AKB}=180^o\)
\(\widehat{AKB}.2=180^o\)
\(\Rightarrow\widehat{AKB}=\frac{180^o}{2}=90^o\) ( 2 )
Từ ( 1 ) và ( 2 ) => AD là đường trung trực của BH
c ) Xét \(\Delta BDI\) và \(\Delta HDC\) có :
\(\widehat{DBI}=\widehat{DHC}\left(=90^o\right)\)
BD = HD ( do \(\Delta ABD=\Delta AHD\) )
\(\widehat{BDI}=\widehat{HDC}\) ( hai góc đối đỉnh )
nên \(\Delta BDI=\Delta HDC\left(g.c.g\right)\)
=> DI = DC
=> \(\Delta DIC\)cân tại D
e ) Gọi M là điểm AD cắt IC
Ta có :
AI = AB + BI
AC = AH + HC
mà AB = AH ( \(\Delta ABD=\Delta AHD\))
BI = HC ( \(\Delta BDI=\Delta HDC\) )
=> AI = AC
=> \(\Delta AIC\) cân tại A
Lại có : \(CB\perp AI\)=> CB là đường cao ứng với cạnh AI
\(IH\perp AC\)=> IH là đường cao ứng với cạnh AC
=> AM là đường cao thứ ba ( hay AD )
=> AM \(\perp\)IC
=> \(AD\perp IC\)
29 tháng 6 2019
Tớ bổ sung ý d) cho Đường Tịch nè:
Ta có : tam giác DIC cân tại D
=> ID = DC
Mà BD = HD (cmt)
=> BD = HD
Mà ta có BC = BD + DC
IH = ID + DH
=> BC = IH
Xét tam giác vuông HIC và tam giác vuông BCI ta có :
BC = IH
IC chung
IBC = CHI = 90 độ
=> Tam giác HIC = tam giác BCI ( g.c.g)
=> BI = HC (tg ứng)
Xét tam giác AKB và tam giác AKH ta có
=> BAD = HAD ( AD là pg)
AK chung
AKB = AKH = 90 độ
=> Tam giác AKB = tam giác AKH (g.c.g)
=> AB = AK
Mà AI = AK + BI
AC = AH + HC
=> AI = AC
=> AIC cân tại A
=> AIC = ACI
Ta có AIC = ACI = 180 - A
Ta có AK = AH (cmt)
=> Tam giác BAH cân tại B
=> ABH = AHB
=> ABH = AHB = 180 - A
=> ABH = AHB = AIC = ACI ( cùng bằng 180 - A)
=> ABH = AIC
Mà 2 góc này ở vị trí đồng vị
=> BH //IC
=> (dpcm)
21 tháng 3 2023
a: Xet ΔABD vuông tại B và ΔAHD vuông tại H có
AD chung
góc BAD=góc HAD
=>ΔABD=ΔAHD
b; AB=AH
DB=DH
=>AD là trung trực của BH
c: Xet ΔDBI vuông tại B và ΔDHC vuông tại H có
DB=DH
góc BDI=góc HDC
=>ΔBDI=ΔHDC
=>DI=DC
=>ΔDIC cân tại D
d: Xét ΔAIC có AB/BI=AH/HC
nên BH//IC
e: AD vuông góc BH
BH//IC
=>AD vuông góc IC
T
12 tháng 4 2019
Hình (tự vẽ)
Xét hai tam giác vuông ABD và AHD có:
\(\widehat{BAD}=\widehat{HAD}\)(AD là phân giác)
AD: cạnh chung
Do đó: ΔABD = ΔAHD (cạnh huyền - góc nhọn)
⇒ BD = DH (cạnh tương ứng)
Xét hai tam giác vuông BID và HCD có:
BD = HD (cmt)
\(\widehat{BID}=\widehat{HCD}\)(đối đỉnh)
Do đó: ΔBID = ΔHCD (cạnh góc vuông - góc nhọn kề)
⇒ DI = DC (hai cạnh tương ứng)
⇒ DIC cân tại D.
KV
3 tháng 2
Do AD là tia phân giác của ∠BAC (gt)
⇒ ∠BAD = ∠CAD
⇒ ∠BAD = ∠HAD
Xét hai tam giác vuông: ∆BAD và ∆HAD có:
AD là cạnh chung
∠BAD = ∠HAD (cmt)
⇒ ∆BAD = ∆HAD (cạnh huyền - góc nhọn)
⇒ BD = HD (hai cạnh tương ứng)
Xét hai tam giác vuông: ∆IBD và ∆CHD có:
BD = HD (cmt)
∠BDI = ∠HDI (đối đỉnh)
⇒ ∆IBD = ∆CHD (cạnh góc vuông - góc nhọn kề)
⇒ BI = HC (hai cạnh tương ứng)
Do ∆BAD = ∆HAD (cmt)
⇒ AB = AH (hai cạnh tương ứng)
⇒ ∆ABH cân tại A
⇒ ∠ABH = ∠AHB = (180⁰ - ∠BAH) : 2 (1)
Ta có:
AI = AB + BI
AC = AH + HC
Mà AB = AH (cmt)
BI = HC (cmt)
⇒ AI = AC
⇒ ∆AIC cân tại A
⇒ ∠AIC = ∠ACI = (180⁰ - ∠IAC) : 2
= (180⁰ - ∠BAH) : 2 (2)
Từ (1) và (2) ⇒ ∠ABH = ∠AIC
Mà ∠ABH và ∠AIC là hai góc đồng vị
⇒ BH // CI
7 tháng 3 2022
a: Xét ΔBAD vuông tại A và ΔBHD vuông tại H có
BD chung
BA=BH
Do đó: ΔBAD=ΔBHD
Suy ra: \(\widehat{ABD}=\widehat{HBD}\)
hay BD là tia phân giác của góc ABC
b: Ta có: AD=DH
mà DH<DC
nên AD<DC
c: Xét ΔADI vuông tại A và ΔHDC vuông tại H có
DA=DH
\(\widehat{ADI}=\widehat{HDC}\)
Do đó: ΔADI=ΔHDC
Suy ra: AI=HC
Ta có: BA+AI=BI
BH+HC=BC
mà BA=BH
và AI=HC
nên BI=BC
hay ΔIBC cân tại I
8 tháng 3 2022
a: BC=15cm
b: Xét ΔBAD vuông tại A và ΔBHD vuông tại H có
BD chung
\(\widehat{ABD}=\widehat{HBD}\)
Do đó:ΔBAD=ΔBHD
c: Xét ΔADK vuông tại A và ΔHDC vuông tại H có
DA=DH
\(\widehat{ADK}=\widehat{HDC}\)
Do đó:ΔADK=ΔHDC
Suy ra: DK=DC và AK=HC
d: Xét ΔBKC có BA/AK=BH/HC
nên AH//KC
23 tháng 4 2023
a: Xet ΔABD vuông tại A và ΔAHD vuông tại H có
AD chung
góc BAD=góc HAD
=>ΔABD=ΔAHD
c: Xét ΔDBI vuông tại B và ΔDHC vuông tại H có
DB=DH
góc BDI=góc HDC
=>ΔBDI=ΔHDC
=>DI=DC và BI=HCC
d: Xét ΔAIC có AB/BI=AH/HC
nên BH//IC
g: BC+AB>AC
=>BC+2AB>AC+AB
mà AB<AD<AC
nên BC>AC+AD-2AB