Cho góc aOb và tia Ot nằm giữa Oa , Ob . Các tia Om,On thứ tự là tia phân giác của góc aOt và bOt . Chứng tỏ rằng \(\widehat{mOn}=\frac{\widehat{aOb}}{2}.\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


* Tìm cách giải
Muốn chứng tỏ tia OK là tia phân giác của góc AOB ta cần chứng tỏ A O K ^ = B O K ^ . Muốn vậy cần chứng tỏ A O N ^ + N O K ^ = B O M ^ + M O K ^ .
* Trình bày lời giải
Ta có O M ⊥ O A ⇒ A O M ^ = 90 ° ; O N ⊥ O B ⇒ B O N ^ = 90 ° .
Tia ON nằm giữa hai tia OA, OM nên A O N ^ + N O M ^ = A O M ^ = 90 ° ;
Tia OM nằm giữa hai tia OB, ON nên B O M ^ + M O N ^ = B O N ^ = 90 ° .
Suy ra A O N ^ = B O M ^ (cùng phụ với M O N ^ ).
Tia OK là tia phân giác của góc MON nên N O K ^ = M O K ^ .
Do đó A O N ^ + N O K ^ = B O M ^ + M O K ^ .(1)
Vì tia ON nằm giữa hai tia OA, OK và tia OM nằm giữa hai tia OB, OK nên từ (1) suy ra A O K ^ = B O K ^ . Mặt khác, tia OK nằm giữa hai tia OA, OB nên tia OK cũng là tia phân giác của góc AOB

a) Ta có :
AOM + BON = 180độ
hay AON + MON + BOM + MON = 180
AON + BOM + 2MON = 180
mà AON + MON + BOM = AOB = 100độ
=> MON + 100 = 180
=> MON = 80độ
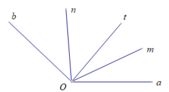
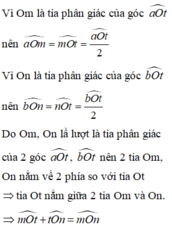
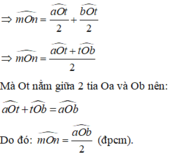
ta có \(Om\) là phân giác của \(\widehat{aOt}\) => \(\widehat{mOt}=\frac{\widehat{aOt}}{2}\)
tương tự ta có \(\widehat{nOt}=\widehat{\frac{bOt}{2}}\)
=> \(\widehat{mOt}+\widehat{nOt}=\frac{\widehat{aOt}+\widehat{bOt}}{2}=\widehat{\frac{aOb}{2}}\)
mà \(Ot\) nằm giữa \(Om\) và \(On\)
=> \(\widehat{mOn}=\widehat{mOt}+\widehat{nOt}=\widehat{\frac{aOb}{2}}\) (ĐPCM)