Với giá trị nguyên nào của x thì biểu thức \(M=\dfrac{17-2x}{7-2x}\) có giá trị lớn nhất
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
24 tháng 4 2023
a: ĐKXĐ: x<>-1
b: \(P=\left(1-\dfrac{x+1}{x^2-x+1}\right)\cdot\dfrac{x^2-x+1}{x+1}\)
\(=\dfrac{x^2-x+1-x-1}{x^2-x+1}\cdot\dfrac{x^2-x+1}{x+1}=\dfrac{x^2-2x}{x+1}\)
c: P=2
=>x^2-2x=2x+2
=>x^2-4x-2=0
=>\(x=2\pm\sqrt{6}\)
8 tháng 12 2021
\(a,ĐK:x\ne\pm2\\ b,A=\dfrac{x^2+4x+4+x^2-4x+4+16}{2\left(x-2\right)\left(x+2\right)}\\ A=\dfrac{2x^2+32}{2\left(x-2\right)\left(x+2\right)}=\dfrac{x^2+16}{x^2-4}\\ c,A=-3\Leftrightarrow-3x^2+12=x^2+16\\ \Leftrightarrow4x^2=-4\Leftrightarrow x\in\varnothing\)
YN
30 tháng 6 2021
\(1.\)
\(-17-\left(x-3\right)^2\)
Ta có: \(\left(x-3\right)^2\ge0\)với \(\forall x\)
\(\Leftrightarrow-\left(x-3\right)^2\le0\)với \(\forall x\)
\(\Leftrightarrow17-\left(x-3\right)^2\le17\)với \(\forall x\)
Dấu '' = '' xảy ra khi:
\(\left(x-3\right)^2=0\)
\(\Leftrightarrow x-3=0\)
\(\Leftrightarrow x=3\)
Vậy \(Max=-17\)khi \(x=3\)
YN
30 tháng 6 2021
\(2.\)
\(A=x\left(x+1\right)+\frac{3}{2}\)
\(A=x^2+x+\frac{3}{2}\)
\(A=\left(x+\frac{1}{2}\right)^2+\frac{5}{4}\)
\(\left(x+\frac{1}{2}\right)^2+\frac{5}{4}\ge\frac{5}{4}\)với \(\forall x\)
\(\Leftrightarrow\left(x+\frac{1}{2}\right)^2+\frac{5}{4}\ge\frac{5}{4}\)với \(\forall x\)
Vậy \(Max=\frac{5}{4}\)khi \(x=\frac{-1}{2}\)
17 tháng 5 2022
a: \(\dfrac{2x-3}{35}+\dfrac{x\left(x-2\right)}{7}\le\dfrac{x^2}{7}-\dfrac{2x-3}{5}\)
\(\Leftrightarrow2x-3+5x\left(x-2\right)\le5x^2-7\left(2x-3\right)\)
\(\Leftrightarrow2x-3+5x^2-10x< =5x^2-14x+21\)
=>-8x-3<=-14x+21
=>6x<=24
hay x<=4
b: \(\dfrac{6x+1}{18}+\dfrac{x+3}{12}>=\dfrac{5x+3}{6}+\dfrac{12-5x}{9}\)
=>2(6x+1)+3(x+3)>=6(5x+3)+4(12-5x)
=>12x+2+3x+9>=30x+18+48-20x
=>15x+11>=10x+66
=>5x>=55
hay x>=11
CM
31 tháng 5 2017
Giá trị của biểu thức 2 x - 3 35 + x x - 2 7 không lớn hơn giá trị của biểu thức x 2 7 - 2 x - 3 5 nghĩa là 2 x - 3 35 + x x - 2 7 ≤ x 2 7 - 2 x - 3 5
Ta có:
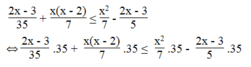
⇔ 2x – 3 + 5 x 2 – 10x ≤ 5 x 2 – 14x + 21
⇔ 2x + 5 x 2 – 10x – 5 x 2 + 14x ≤ 21 + 3
⇔ 6x ≤ 24
⇔ x ≤ 4
Vậy với x ≤ 4 thì giá trị của biểu thức 2 x - 3 35 + x x - 2 7 không lớn hơn giá trị của biểu thức x 2 7 - 2 x - 3 5
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
8 tháng 4 2023
A = \(\dfrac{2x-1}{x+2}\)
a, A là phân số ⇔ \(x\) + 2 # 0 ⇒ \(x\) # -2
b, Để A là một số nguyên thì 2\(x-1\) ⋮ \(x\) + 2
⇒ 2\(x\) + 4 - 5 ⋮ \(x\) + 2
⇒ 2(\(x\) + 2) - 5 ⋮ \(x\) + 2
⇒ 5 ⋮ \(x\) + 2
⇒ \(x\) + 2 \(\in\) { -5; -1; 1; 5}
⇒ \(x\) \(\in\) { -7; -3; -1; 3}
c, A = \(\dfrac{2x-1}{x+2}\)
A = 2 - \(\dfrac{5}{x+2}\)
Với \(x\) \(\in\) Z và \(x\) < -3 ta có
\(x\) + 2 < - 3 + 2 = -1
⇒ \(\dfrac{5}{x+2}\) > \(\dfrac{5}{-1}\) = -5 ⇒ - \(\dfrac{5}{x+2}\)< 5
⇒ 2 - \(\dfrac{5}{x+2}\) < 2 + 5 = 7 ⇒ A < 7 (1)
Với \(x\) > -3; \(x\) # - 2; \(x\in\) Z ⇒ \(x\) ≥ -1 ⇒ \(x\) + 2 ≥ -1 + 2 = 1
\(\dfrac{5}{x+2}\) > 0 ⇒ - \(\dfrac{5}{x+2}\) < 0 ⇒ 2 - \(\dfrac{5}{x+2}\) < 2 (2)
Với \(x=-3\) ⇒ A = 2 - \(\dfrac{5}{-3+2}\) = 7 (3)
Kết hợp (1); (2) và(3) ta có A(max) = 7 ⇔ \(x\) = -3
\(M=\dfrac{17-2x}{7-2x}=\dfrac{2x-17}{2x-7}=\dfrac{2x-7-10}{2x-7}\)
\(=1-\dfrac{10}{2x-7}\)
Để M lớn nhất thì \(-\dfrac{10}{2x-7}\) lớn nhất
=>\(\dfrac{10}{2x-7}\) nhỏ nhất
=>2x-7=-1
=>2x=6
=>x=3