1. Cho hình thang ABCD, AB là đáy nhỏ, góc A= 900. CMR:
a) AC > BD
b) AC2 -BD2 = CD2 - AB2
2. Cho tam giác ABC vuông tại tại A. Các đường trung tuyến AD và BE vuông góc với nhau tại G. Biết AB = √6 cm. Tính BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
13 tháng 4 2018
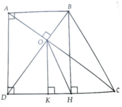
a, Tính được DB=15cm. A D B ^ ≈ 37 0 ; A B D ^ ≈ 53 0
b, Tính được AO=7,2cm, DO=9,6cm và AC=20cm
c, Kẻ OK ⊥ DC tại K
DH=AB=9cm, DC=16cm, DK=5,76cm và OK=7,68cm
Từ đó S D O H = O K . D H 2 = 7 , 68 . 9 2 = 34,56 c m 2
5 tháng 6 2017
Câu 1: Tam giác ABC vuông tại A có AM là đường trung tuyến ứng với cạnh huyền BC
=> AM=\(\frac{1}{2}\)BC mà AM=6 cm=> BC=12cm.
Tam giác ANB vuông tại A có AN2+AB2=BN2 (Theo Pytago) mà BN=9cm (gt)
=>AN2+AB2=81 Lại có AN=\(\frac{1}{2}\)AC =>\(\frac{1}{2}\)AC2+AB2=81 (1)
Tam giác ABC vuông tại A có: AC2+AB2=BC2 => BC2 - AB2 = AC2 (2)
Từ (1) và (2) suy ra \(\frac{1}{4}\)* (BC2 - AB2)+AB2=81 mà BC=12(cmt)
=> 36 - \(\frac{1}{4}\)AB2+AB2=81
=> 36+\(\frac{3}{4}\)AB2=81
=> AB2=60=>AB=\(\sqrt{60}\)
9 tháng 7 2019
C2
Cho hình thang cân ABCD có đáy lớn CD = 1
C4
Câu hỏi của Thiên An - Toán lớp 9 - Học toán với OnlineMath
18 tháng 5 2018
\(\text{Xét: }\Delta BGA\perp G\text{ thì }BG^2+GA^2=AB^2\)
\(\Leftrightarrow\frac{4}{9}\left(BE^2+AD^2\right)=AB^2\)
\(\Leftrightarrow BE^2+\frac{1}{4}BC^2=\frac{27}{2}\)(1)
\(\text{Có trong: }\Delta ABE\text{ thì }AB^2+AE^2\)
\(\Leftrightarrow6+\frac{1}{4}AC^2=BE^2\)(2)
Từ (1) và (2), ta có:
\(BC^2+AC^2=30\left(cm\right)\)
Mà: \(BC^2-AC^2=AB^2=6\left(cm\right)\)
Nên \(BC^2=18\)
\(\Rightarrow BC=3\sqrt{2}\left(cm\right)\)
18 tháng 5 2018
Áp dụng Pitago cho tg ABG
Áp dụng Pitago cho tg BDG
Tiếp tục làm tiếp nha bạn :")
AT
12 tháng 6 2021
Bài 1:
a.
AB // CD
=> A + D = 1800 (2 góc trong cùng phía)
=> A = 1800 - D = 1800 - 540 = 1260
AB // CD
=> B + C = 1800 (2 góc trong cùng phía)
=> B = 1800 - C = 1800 - 1050 = 750
b.
AB // CD
=> A + D = 1800 (2 góc trong cùng phía)
=> A = (1800 - 320) : 2 = 740
=> D = 1800 - 740 = 1060
AB // CD
=> B + C = 1800 (2 góc trong cùng phía)
=> B = 1800 : (1 + 2) . 2 = 1200
=> C = 1800 - 1200 = 600
6 tháng 8 2022
Bài 2:
a: Xét ΔABE và ΔACF có
góc ABE=góc ACF
AB=AC
góc A chung
Do đó: ΔABE=ΔACF
Suy ra: AE=AF
b: Xét ΔABC có AF/AB=AE/AC
nên FE//BC
=>BFEC là hình thang
mà CF=BE
nên BFEC là hình thang cân
c: Xét ΔFEB có góc FEB=góc FBE
nên ΔFEB cân tại F
=>FE=FB=EC
DD
Đoàn Đức Hà
Giáo viên
21 tháng 6 2021
Xét tam giác \(BGA\)vuông tại \(G\):
\(BA^2=BG^2+GA^2=\frac{4}{9}\left(BE^2+AM^2\right)\Leftrightarrow BE^2+\frac{BC^2}{4}=\frac{27}{2}\)(1)
Xét tam giác \(ABE\)vuông tại \(A\):
\(BE^2=AB^2+AE^2=6+\frac{1}{4}AC^2\)(2)
Từ (1) và (2) suy ra \(BC^2+AC^2=30\)
mà \(BC^2=AC^2+6\)
suy ra \(BC^2=18\Rightarrow BC=3\sqrt{2}\left(cm\right)\).