Giúp em
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
T
11
29 tháng 9 2018
\(\left(x-1\right)\left(3x-15\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x-1=0\\3x-15=0\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}x=1\\x=5\end{cases}}\)
Vậy x = { 1; 5 }
TA
1
LT
2
NT
3
26 tháng 9 2021
\(A=\left(\dfrac{\sqrt{x}+1}{\sqrt{x}-1}-\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\right)\left(1-\dfrac{1}{\sqrt{x}}\right)\left(đk:x>0,x\ne1\right)\)
\(=\dfrac{\left(\sqrt{x}+1\right)^2-\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}.\dfrac{\sqrt{x}-1}{\sqrt{x}}\)
\(=\dfrac{x+2\sqrt{x}+1-x+2\sqrt{x}-1}{\sqrt{x}\left(\sqrt{x}+1\right)}\)
\(=\dfrac{4\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+1\right)}=\dfrac{4}{\sqrt{x}+1}\)
TM
1
BT
7
13 tháng 7 2021
1) Ta có: \(\sqrt{2x+5}=\sqrt{3-x}\)
\(\Leftrightarrow2x+5=3-x\)
\(\Leftrightarrow2x+x=3-5\)
\(\Leftrightarrow3x=-2\)
hay \(x=-\dfrac{2}{3}\)
2) Ta có: \(\sqrt{2x-5}=\sqrt{x-1}\)
\(\Leftrightarrow2x-5=x-1\)
\(\Leftrightarrow2x-x=-1+5\)
\(\Leftrightarrow x=4\)
PN
23 tháng 8 2021
3 , \(PT\left(đk:\frac{16}{3}\ge x\ge3\right)< =>x^2-3x=16-3x\)
\(< =>x^2-16=0< =>\left(x-4\right)\left(x+4\right)=0< =>\orbr{\begin{cases}x=4\left(tm\right)\\x=-4\left(ktm\right)\end{cases}}\)
4 , \(PT\left(đk:...\right)< =>2x^2-3=4x-3< =>2x^2-4x=0\)
\(< =>2x\left(x-2\right)=0< =>\orbr{\begin{cases}x=0\left(...\right)\\x=2\left(...\right)\end{cases}}\)
bạn tự tìm đk rồi đối chiếu nhé :P
BT
5
13 tháng 7 2021
1) Ta có: \(\sqrt{4x}=\sqrt{5}\)
nên 4x=5
hay \(x=\dfrac{5}{4}\)
2) Ta có: \(\sqrt{16x}=8\)
nên 16x=64
hay x=4
PN
23 tháng 8 2021
3, \(2\sqrt{x}=\sqrt{9x}-3\left(đk:x\ge0\right)\)
\(< =>2\sqrt{x}-3\sqrt{x}+3=0\)
\(< =>3-\sqrt{x}=0< =>x=9\)(tmđk)
4, \(\sqrt{3x-1}=4\left(đk:x\ge\frac{1}{3}\right)\)
\(< =>3x-1=16< =>3x-17=0\)
\(< =>x=\frac{17}{3}\)(tmđk)
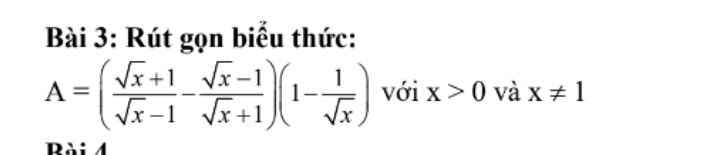
Bài 58b;
D = \(\dfrac{3^9.2^{10}}{6^8}\): (\(\dfrac{5^5.2^4}{10^4}.\dfrac{2^6.3^4}{6^4}\))
D = \(\dfrac{\left(3.2\right)^9.2}{6^8}\):(\(\dfrac{\left(5.2\right)^4.5}{10^4}\).\(\dfrac{\left(2.3\right)^4.2^2}{6^4}\))
D = \(\dfrac{6^9.2}{6^8}\): (\(\dfrac{10^4.5}{10^4}\).\(\dfrac{6^4.4}{6^4}\))
D = 6.2 : (5.4)
D = 12:20
D = \(\dfrac{3}{5}\)
Bài 55b;
B = \(\dfrac{18}{2.5}\) + \(\dfrac{18}{5.8}\) + ... + \(\dfrac{18}{203.206}\)
B = 6.(\(\dfrac{3}{2.5}\) + \(\dfrac{3}{5.8}\) + ... + \(\dfrac{3}{203.206}\))
B = 6.(\(\dfrac{1}{2}\) - \(\dfrac{1}{5}\) + \(\dfrac{1}{5}\) - \(\dfrac{1}{8}\) + ... + \(\dfrac{1}{203}\) - \(\dfrac{1}{206}\))
B = 6.(\(\dfrac{1}{2}\) - \(\dfrac{1}{206}\))
B = 6.\(\dfrac{51}{103}\)
B = \(\dfrac{306}{103}\)