Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) 
b) ta có MD là tia phân giác của \(\widehat{AMB}\), ME là tia phân giác của \(\widehat{AMC}\)
=> \(\widehat{AMD}=\widehat{DMB}=\dfrac{1}{2}\widehat{AMB}\) và \(\widehat{AME}=\widehat{EMC}=\dfrac{1}{2}\widehat{AMC}\)
=> \(\widehat{AME}+\widehat{AMD}=\dfrac{\widehat{AMC}+\widehat{AMB}}{2}=\dfrac{180^o}{2}=90^o\)
Ta có \(\widehat{EMC}=\widehat{MED}\)(do ED//BC)
mà \(\widehat{EMC}=\widehat{EMI}\)
=> \(\widehat{EMI}=\widehat{MEI}\)=> tam giác EIM cân tại I
=> EI=IM
cmtt : IM=ID
=> EI=IM=MD
=> IM = \(\dfrac{1}{2}\left(EI+ID\right)=\dfrac{1}{2}ED\)(ĐPCM)
1: Xet ΔMAB co MD là phân giác
nen AD/DB=AM/MB=AM/MC
Xét ΔMCA có ME là phân giác
nên AE/EC=AM/MC=AD/DB
=>DE//BC
2: Xét ΔABM có DG//BM
nên DG/BM=AG/AM
Xét ΔACM có EG//MC
nên EG/MC=AG/AM
=>DG/BM=EG/MC
mà BM=MC
nên DG=EG
=>G là trung điểm của DE
Để G là trung điểm của AM thì ADME là hình bình hành
=>DM//AC
=>D là trung điểm của AB
=>E là trung điểm của BC
=>AM/MB=AD/DB=1
=>AM=1/2BC
=>góc BAC=90 độ
Hình bạn tự vẽ nha.
a, \(\Delta ABC\) có: AM là đường trung tuyến của \(\Delta ABC\)\(\Rightarrow BM=MC\), \(AI=\frac{2}{3}AM\)
\(\Delta AMB\)có: MD là phân giác của \(\widehat{AMB}\)\(\Rightarrow\frac{AD}{DB}=\frac{AM}{MB}\)(tính chất đường phân giác trong tam giác) (1)
\(\Delta AMC\)có: ME là phân giác của \(\widehat{AMC}\)\(\Rightarrow\frac{AE}{EC}=\frac{AM}{MC}\)(tính chất đường phân giác trong tam giác) (2)
Từ (1), (2) và \(BM=MC\left(cmt\right)\Rightarrow\frac{AD}{DB}=\frac{AE}{EC}\)
\(\Delta ABC\)có: \(\frac{AD}{DB}=\frac{AE}{EC}\left(cmt\right)\Rightarrow DE//BC\)(định lý Ta-lét đảo)
b, \(\Delta ABM\)có: \(DI//BM\left(cmt\right)\Rightarrow\frac{DI}{BM}=\frac{AI}{AM}\)(hệ quả của định lý Ta-lét) (3)
\(\Delta AMC\)có: \(IE//MC\left(cmt\right)\Rightarrow\frac{IE}{CM}=\frac{AI}{AM}\)(hệ quả của định lý Ta-lét) (4)
Từ (3), (4) và \(BM=MC\left(cmt\right)\Rightarrow DI=IE\)
c, Ta có: \(\frac{IE}{CM}=\frac{AI}{AM}\left(cmt\right)\)\(\Leftrightarrow\frac{IE}{15}=\frac{\frac{2}{3}AM}{AM}\)\(\Leftrightarrow\frac{IE}{15}=\frac{\frac{2}{3}.10}{10}\)\(\Leftrightarrow\frac{IE}{15}=\frac{2}{3}\)\(\Leftrightarrow IE=10\left(cm\right)\)
a: Xét ΔMAB có MD là phân giác
nên AD/DB=AM/MB=AM/MC
Xét ΔAMC có ME là phân giác
nên AE/EC=AM/MC
=>AD/DB=AE/EC
=>ED//BC
b: Xét ΔABM có DI//BM
nên DI/BM=AI/AM
Xét ΔACM có EI//MC
nên EI/CM=AI/AM
=>DI/BM=EI/CM
=>DI=EI
a) Xét ΔAMB có
MD là đường phân giác ứng với cạnh AB(gt)
nên \(\dfrac{MB}{MA}=\dfrac{BD}{AD}\)(Định lí Tia phân giác)
⇒\(\dfrac{MB}{4}=\dfrac{1.5}{3}=\dfrac{1}{2}\)
hay MB=2(cm)
Vậy: MB=2cm
AD/DB=AM/MB
AE/EC=AM/MC
mà MB=MC
nên AD/DB=AE/EC
=>DE//BC
Để DE là đừog trung bình của ΔABC thì AD/DB=AE/EC=1
=>AM/MB=AM/MC=1
=>ΔABC vuông tại A
Vì DI = IE (cmt) nên MI là đường trung tuyến của tam giác MDE.
ΔMDE vuông (vì MD, ME là tia phân giác của góc kề bù) nên MI = DI = IE
Đặt DI = MI = x, ta có D I B M = A I A M (cmt) nên x 15 = 10 − x 10
Từ đó x = 6 suy ra DE = 12cm
Đáp án: D
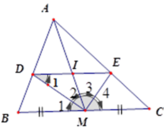
a: Xét ΔMAB có MD là phân giác
nên \(\dfrac{AD}{DB}=\dfrac{AM}{MB}=\dfrac{AM}{MC}\left(1\right)\)
Xét ΔMAC có ME là phân giác
nên \(\dfrac{AE}{EC}=\dfrac{AM}{MC}\left(2\right)\)
Từ (1),(2) suy ra \(\dfrac{AD}{DB}=\dfrac{AE}{EC}\)
Xét ΔABC có \(\dfrac{AD}{DB}=\dfrac{AE}{EC}\)
nên DE//BC
b: Xét ΔABM có DI//BM
nên \(\dfrac{DI}{BM}=\dfrac{AI}{AM}\left(3\right)\)
Xét ΔAMC có IE//MC
nên \(\dfrac{IE}{MC}=\dfrac{AI}{AM}\left(4\right)\)
Từ (3),(4) suy ra \(\dfrac{DI}{BM}=\dfrac{IE}{MC}\)
mà BM=MC(M là trung điểm của BC)
nên DI=IE
=>I là trung điểm của DE