Cho tam giác MNP vuông tại M có MN = 6 cm. Trên tia MN lấy các điểm D , E sao cho MD = 3 cm, ME = 8 cm.
a) So sánh độ dài PD và PE .
b) Sắp xếp các đoạn thẳng PD , PE , PN theo thứ tự có độ dài tăng dần.
Em cần gấp
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: PN=10cm
b: Xét ΔPMK vuông tại M và ΔPEK vuông tại E có
PK chung
\(\widehat{MPK}=\widehat{EPK}\)
Do đó: ΔPMK=ΔPEK
c: Xét ΔMKD vuông tại M và ΔEKN vuông tại E có
KM=KE
\(\widehat{MKD}=\widehat{EKN}\)
DO đó: ΔMKD=ΔEKN
Suy ra: KD=KN
d: Ta có: PM+MD=PD
PE+EN=PN
mà PM=PE
và MD=EN
nên PD=PN
hayΔPDN cân tại P

a: ΔDEF vuông tại D
=>góc DEF<90 độ
=>góc FEP>90 độ
=>FE<FP
góc FEP>90 độ
=>góc FPE<90 độ
=>góc FPQ>90 độ
=>FP<FQ
b: FE<FP
FP<FQ
=>FE<FP<FQ

a: NP=5cm
b: Xét ΔEMD có
EN là đường cao
EN là đường trug tuyến
Do đó: ΔEMD cân tại E

a)xét tam giác(tg) mne và tg mpd có
mn=mp(gt)
me=md(_)
m góc chung
=>tg mne = tg mpd
b)có md+dn+180(2 góc kề bù)
me+ep=180(_________)
mà md=me=>dn=ep
vì tg mne= tg mpd(cma)=>dnk=kpe(2 góc t/ư)
và men=ndp(2 góc t/ư)mà men+pen=mdp+ndp=180(kề bù) và men=ndp=>pen=mdp
xét tg dkn và tg ekp có
ndk=kpe(cmt)
dn=ep(cmt)
pen=mdp(cmt)
=>tgdkn=tg ekp
a) Xét MNE và MPD:
MN=MP(giả thiết)
góc NMP chung
ME=MD(giả thiết)
=> tam giác MNE=MPD(c.g.c)
b) Do tam giác MNE=MPD=> góc MNE= MPD và góc MEN=MDP (1)
=> góc NDP=NEP (cùng bù với 2 góc bằng nhau)
do MN=MP và MD=ME => ND=EP (2)
từ (1) và (2) => tam giác DKN=EKP (g.c.g)
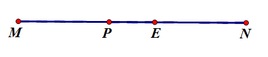
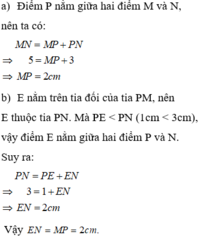
a) Ta có tam giác MNP vuông tại M, với MN = 6 cm, MD = 3 cm, ME = 8 cm. Ta cần so sánh độ dài PD và PE.
Vì tam giác MNP vuông tại M, ta có hai tam giác vuông nhỏ MDP và MEP.
Theo định lý Pythagoras trong tam giác vuông, ta có:
- Trong tam giác MDP: MP² = MD² + DP²
=> MP = √(MD² + DP²) = √(3² + DP²) = √(9 + DP²)
- Trong tam giác MEP: MP² = ME² + EP²
=> MP = √(ME² + EP²) = √(8² + EP²) = √(64 + EP²)
Vì MP là đoạn thẳng cố định, nên ta có: √(9 + DP²) = √(64 + EP²)
=> 9 + DP² = 64 + EP²
=> DP² - EP² = 55
=> DP² > EP²
=> DP > EP
Vậy ta kết luận rằng độ dài của đoạn thẳng PD lớn hơn độ dài của đoạn thẳng PE.
b) Để sắp xếp các đoạn thẳng PD, PE, PN theo thứ tự có độ dài tăng dần, ta cần tính độ dài của đoạn thẳng PN.
Trong tam giác vuông MNP, ta áp dụng định lý Pythagoras:
PN² = MN² + MP²
=> PN = √(MN² + MP²) = √(6² + MP²) = √(36 + MP²)
Với MP = √(9 + DP²), ta có: PN = √(36 + 9 + DP²) = √(45 + DP²)
Để sắp xếp các đoạn thẳng theo thứ tự tăng dần, ta cần so sánh độ dài của chúng. Ta đã biết rằng DP > EP, nên để sắp xếp tăng dần, ta có: PE < PN < PD.
Vậy thứ tự các đoạn thẳng là: PE < PN < PD.