Question

[Lê Ngọc Minh Châu]

Cho tam giác ABC vuông tại A, BD là phân giác của góc B (D thuộc AC).Kẻ DE vuông với BC tại E.

a)Chứng minh BA=BE

b)Chứng minh BD là đường trung trực của AE

c)Kẻ Bx vuông góc với BD(Bx nằm trên nửa mặt phẳng bờ BD không chứa A),trên tia Bx lấy H sao cho BH=AE

CMR HE vuông góc với AC

d)O là trung điểm của BE.Chứng minh A,O,H thẳng hàng

Answer 1

[Nguyễn Thị Thương Hoài]

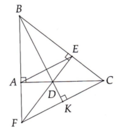
a; Xét tam giác vuông ABD và tam giác vuông  EBD có

\(\widehat{ABD}\) = \(\widehat{EBD}\) (vì BD là phân giác của góc B)

Cạnh BD chung

⇒\(\Delta\)ABD = \(\Delta\)EBD (cạnh huyền góc nhọn)

⇒ BA = BE (đpcm)

b; BA = BE (cmt)

   ⇒\(\Delta\)ABE cân tại B

    BD là phân giác góc ABE

    ⇒ BD là đường trung trực của AE vì trong tam giác đường phân giác cũng là đường trung trực)

c; BD \(\perp\)BH (gt)

    BD \(\perp\)AE (cmt)

⇒ BH//AE (vì hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì song song với nhau)

Xét tứ giác ABHE có

    BH//AE (cmt)

    BH = AE (gt)

⇒ Tứ giác ABHE là hbh (vì tứ giác có một cặp cạnh đối diện song song và bằng nhau thì tứ giác đó là hình hình bình hành)

⇒ AB//HE 

  ⇒ AC \(\perp\) HE (Vì một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng còn lại.)

  d; Tứ giác ABHE là hình bình hành 

       O là trung điểm BE 

      ⇒ O là trung điểm của AH

     Vì hình bình hành có hai đường chéo cắt nhau tại trung điểm mỗi đường.

      ⇒ A; O; H thẳng hàng (đpcm)