giup em bai 3 cam on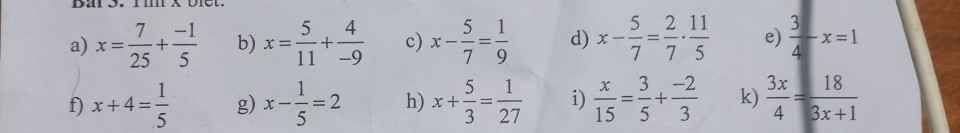
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Cách làm ngắn gọn: \(5=\dfrac{5\left(x-1\right)}{x-1}=\dfrac{5x-5}{x-1}=\dfrac{5x+5-10}{x-1}\)
Do đó chọn \(f\left(x\right)=5x+5\) thế vào nhanh chóng tính ra kết quả giới hạn
Còn cách khác phức tạp hơn (có thể sử dụng cho tự luận):
Do \(\lim\limits_{x\rightarrow1}\dfrac{f\left(x\right)-10}{x-1}=5\) hữu hạn nên \(f\left(x\right)-10=0\) có nghiệm \(x=1\)
\(\Rightarrow f\left(1\right)-10=0\Rightarrow f\left(1\right)=10\)
Do đó:
\(\lim\limits_{x\rightarrow1}\dfrac{f\left(x\right)-10}{\left(\sqrt{x}-1\right)\left(\sqrt{4f\left(x\right)+9}+3\right)}=\lim\limits_{x\rightarrow1}\dfrac{\left[f\left(x\right)-10\right]\left(\sqrt{x}+1\right)}{\left(x-1\right)\left(\sqrt{4f\left(x\right)+9}+3\right)}\)
\(=\lim\limits_{x\rightarrow1}\dfrac{f\left(x\right)-10}{x-1}.\dfrac{\sqrt{x}+1}{\sqrt{4f\left(x\right)+9}+3}=5.\dfrac{1+1}{\sqrt{4f\left(1\right)+9}+3}=5.\dfrac{2}{\sqrt{4.10+9}+3}=...\)



Em rất thích xem bộ phim Đất rừng phương Nam chiếu trên màn ảnh nhỏ. Đây là bộ phim được dàn dựng từ tác phẩm nổi tiếng của Đoàn Giỏi – một nhà văn chuyên viết về đề tài thiên nhiên và con người vùng đồng bằng miền Tây Nam Bộ thời kì chống Pháp xâm lược.
Tác phẩm Đất rừng phương Nam được sáng tác vào năm 1957, sau khi nhà văn Đoàn Giỏi tập kết ra Bắc. Tác giả đã đem đến cho người đọc những hiểu biết mới mẻ và phong phú, từ đó thêm yêu mến thiên nhiên và con người ở mảnh đất tận cùng của Tổ quốc. Đoạn văn Sông nước Cà Mau trích từ chương XVIII của tác phẩm nói trên.
Qua đoạn văn này, em nhận thấy rằng đất mũi Cà Mau có vẻ đẹp rộng lớn, hùng vĩ và đầy sức sống hoang dã. Chợ Năm Căn là hình ảnh tiêu biểu cho cuộc sống tấp nập, trù phú, độc đáo ở vùng đất tận cùng phía Nam Tổ quốc.
Đọc đoạn văn này, em có cảm tưởng như được cùng với chú bé An (nhân vật chính của truyện) ngồi trên con thuyền len lỏi qua các kênh rạch chằng chịt như mạng nhện của rừng u Minh để rồi đổ ra sông Cửa Lớn, xuôi về Năm Căn. Cả một không gian rộng lớn được bao phủ bởi một màu xanh bất tận: trên thì trời xanh, dưới thì nước xanh, chung quanh cũng chỉ toàn một sắc xanh cây lá.
Âm thanh đặc trưng của xứ sở này là tiếng rì rào bất tận của những khu rừng đước bạt ngàn, cùng tiếng sóng ì ầm từ biển Đông và vịnh Thái Lan ngày đêm không ngớt vọng về trong hơi gió muối…
Tên đất, tên sông ở đây thật mộc mạc, giản dị: gọi là rạch Mái Giầm vì hai bên bờ rạch mọc toàn những cây mái giầm cọng tròn xốp nhẹ, trên chỉ xòa ra độc một cái lá xanh hình chiếc bơi chèo nhỏ; gọi là kênh Bọ Mắt vì ở đó tụ tập không biết cơ man nào là bọ mắt, đen như hạt vừng, chúng cứ bay theo thuyền từng bầy như những đám mây nhỏ… Gọi là kênh Ba Khía vì ở đó hai bên bờ tập trung toàn những con ba khía, chúng bám đặc sệt quanh các gốc cây… Còn như xã Năm Căn thì nghe nói ngày xưa trên bờ sông chỉ độc có một cái lán năm gian của những người tới đốn củi hầm than dựng nên, cũng như Cà Mau là nói trại đi theo chữ “tức khơ mâu” tiếng Miên, nghĩa là “nước đen”
Mấy trăm đời lấn luôn ra biển…
Mũi thuyền xé sóng – mũi Cà Mau.

\(\frac{1}{1.4}+\frac{1}{4.7}+\frac{1}{7.10}+...+\frac{1}{40.43}+\frac{1}{43.46}\)
\(=3.\left(1-\frac{1}{4}+\frac{1}{4}-\frac{1}{7}+\frac{1}{7}-\frac{1}{10}+...+\frac{1}{43}-\frac{1}{46}\right)\)
\(=3.\left(1-\frac{1}{46}\right)\)
\(=3.\frac{45}{46}\)
\(=\frac{135}{46}\)
~Học tốt~

a; \(\dfrac{x-1}{12}\) = \(\dfrac{5}{3}\)
\(x-1\) = \(\dfrac{5}{3}\) \(\times\) 12
\(x\) - 1 = 20
\(x\) = 20 + 1
\(x\) = 21
b; \(\dfrac{-x}{8}\) = \(\dfrac{-50}{x}\)
-\(x\).\(x\) = -50.8
-\(x^2\) = -400
\(x^2\) = 400
\(\left[{}\begin{matrix}x=-20\\x=20\end{matrix}\right.\)
Vậy \(x\) \(\in\) {-20; 20}
c; \(\dfrac{x}{3}\) = \(\dfrac{14}{x+1}\)
\(x\).(\(x\)+1) = 14.3
\(x^2\) + \(x\) = 42
\(x^2\) + \(x\) - 42 = 0
\(x^2\) - 6\(x\) + 7\(x\) - 42 = 0
\(x\).(\(x\) - 6) + 7.(\(x\) - 6) = 0
(\(x\) - 6).(\(x\) + 7) = 0
\(\left[{}\begin{matrix}x-6=0\\x+7=0\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=6\\x=-7\end{matrix}\right.\)
Vậy \(x\) \(\in\) {-7; 6}
d; \(x-\dfrac{2}{9}\) = \(\dfrac{1}{6}\)
\(x\) = \(\dfrac{1}{6}\) + \(\dfrac{2}{9}\)
\(x\) = \(\dfrac{7}{18}\)
Vậy \(x\) = \(\dfrac{7}{18}\)





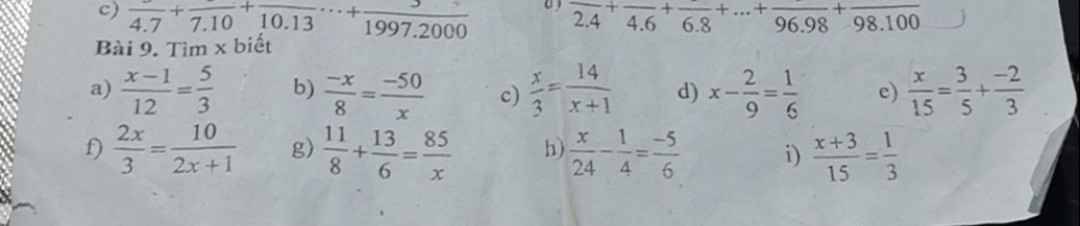

a; \(x\) = \(\dfrac{7}{25}\) + \(\dfrac{-1}{5}\)
\(x\) = \(\dfrac{7}{25}\) - \(\dfrac{5}{25}\)
\(x=\dfrac{2}{25}\)
b; \(x=\dfrac{5}{11}\) + \(\dfrac{4}{-9}\)
\(x=\dfrac{45}{99}-\dfrac{44}{99}\)
\(x=\dfrac{1}{99}\)
c; \(x\) - \(\dfrac{5}{7}\) = \(\dfrac{1}{9}\)
\(x\) = \(\dfrac{1}{9}\) + \(\dfrac{5}{7}\)
\(x=\dfrac{7}{63}+\dfrac{45}{63}\)
\(x\) = \(\dfrac{52}{63}\)