a,b,c là số nguyên đơn biết A B C * 8 = A C C C tính A+B+C+8 = ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Từ 2 giả thiết: \(a+b+c=2018;\frac{1}{a+b}+\frac{1}{b+c}+\frac{1}{c+a}=\frac{6}{2018}\)
\(\Rightarrow\left(a+b+c\right).\left(\frac{1}{a+b}+\frac{1}{b+c}+\frac{1}{c+a}\right)=\frac{2018.6}{2018}=6\)
\(\Leftrightarrow\frac{a+b+c}{a+b}+\frac{a+b+c}{b+c}+\frac{a+b+c}{c+a}=6\)
\(\Leftrightarrow1+\frac{c}{a+b}+1+\frac{a}{b+c}+1+\frac{b}{c+a}=6\)
\(\Leftrightarrow\frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}=3\)
Vậy giá trị của biểu thức đó là 3.

Vì a lớn hơn b 1 đơn vị nên a = b + 1
Vì b bé hơn c 4 đơn vị nên c = b+ 4
thay a = b +1 ; c = b= 4 vào biểu thức a + b + c = 11 ta có
a + b + c = ( b + 1 ) + b + ( b + 4 )
= b + 1 + b + b + 4
= b + b + b + 5
= 3 x b + 5 = 11
3 x 5 = 11 - 5
3 x b = 6
b = 6 : 3
b = 2
Thay b = 2 vào a = b+ 1 ta có a = 2 + 1 = 3
Thay b = 2 vào c = b + 4 ta có c = 2 + 4 = 6
Vậy số abc cần tìm là 326
Học tốt
#Gấu

Chọn A
Hàm số f(x) = (x-6) x 2 + 4 xác định và liên tục trên đoạn [0;3].
![]()
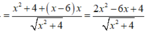

![]()
Suy ra ![]()
![]()
![]() với a là số nguyên và b, c là các số nguyên dương nên
với a là số nguyên và b, c là các số nguyên dương nên
a = - 12, b = 3, c = 13. Do đó: S = a + b + c = 4.

\(f\left(x\right)=ax^2+bx+c\Rightarrow\hept{\begin{cases}f\left(0\right)=c\\f\left(1\right)=a+b+c\\f\left(2\right)=4a+2b+c\end{cases}}\)
\(f\left(0\right)\) nguyên \(\Rightarrow c\) nguyên \(\Rightarrow\hept{\begin{cases}2a+2b\\4a+2b\end{cases}}\) nguyên
\(\Rightarrow\left(4a+2b\right)-\left(2a+2b\right)=2a\)(nguyên)
\(\Rightarrow2b\) nguyên
\(\Rightarrowđpcm\)
