Chứng minh định lí tổng 4 góc của 1 tứ giác bằng 360 ( không dùng cách kẻ đường chéo)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NH
1
TB
4
24 tháng 8 2018
Bởi vì nếu vẽ bất cứ một đường chéo nào trên tứ giác thì đều chia tứ giác thành hai tam giác. Mà tổng các góc trong 1 tam giác bằng 180 độ suy ra tổng các góc trong 1 tứ giác bằng 180. 2=360 độ
NP
0
22 tháng 3 2021
a) Xét (O) có
ΔACD nội tiếp đường tròn(A,C,D\(\in\)(O))
AD là đường kính(gt)
Do đó: ΔACD vuông tại C(Định lí)
Suy ra: AC\(\perp\)CD tại C
hay \(EC\perp CD\) tại C
Xét tứ giác ECDF có
\(\widehat{EFD}\) và \(\widehat{ECD}\) là hai góc đối
\(\widehat{EFD}+\widehat{ECD}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: ECDF là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
TD
1
7 tháng 9 2021
Gọi A^1, B^1, C^1 là 3 góc trong của tam giác ABC. A^2, B^2,C^2 là 3 góc ngoài của tam giác ABC.
Ta có: A^1 + A^2 = 180* B^1 + B^2 = 180* C^1 + C^2 = 180*
---------------------
Cộng vế theo vế được: A^1 +B^1 +C^1 +A^2 +B^2 +C^2 = 3.180* mà A^1 +B^1 +C^1 = 180* (tổng 3 góc trong của tam giác)
=> A^2 +B^2 +C^2 = 3.180* - 180* = 2.180* = 360*
9 tháng 10 2018
Giả sử tứ giác đó là ABCE, các điểm M,N,P,Q ,E,F lần lượt là trung điểm của các đoạn : AB, BC,CD, DA ,BD và AC
Ta chứng minh được EMFP, QENF, MNPQ là hình bình hành ( cái này chỉ cần sử dụng đường trung bình là được )
từ đó suy ra MP, QN, EF đồng qui tại trung điểm G của EF ( vì 3 hình bình hành trên đồng tâm )
GH
Gia Hân
VIP
18 tháng 7 2023
Bài 1:
a) Sử dụng tính chất tổng hai cạnh trong một tam giác thì lớn hơn cạnh còn lại cho các tam giác OAB, OBC,OCD và ODA.
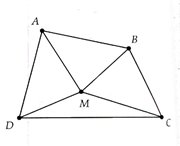
b) Chứng minh tổng hai đường chéo lớn hơn nửa chu vi tứ giác sử dụng kết quả của a).
Chứng minh tổng hai đường chéo nhỏ hơn chu vi tứ giác sử dụng tính chất tổng hai cạnh trong một tam giác thì lớn hơn cạnh còn lại cho các tam giác ABC, ADC, ABD và CBD
Bài 3:
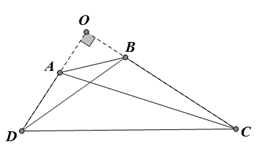
Gọi O là giao điểm AD và BC.
Ta có nên
Áp dụng định lí Py – ta – go,
Ta có
Nên
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
15 tháng 7 2023
Bài 1: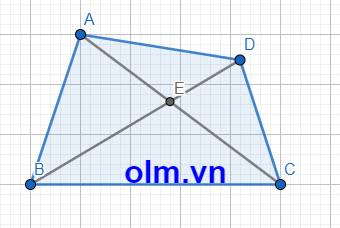 
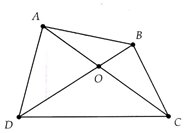
Gọi E là giao điểm của hai đường chéo AC và BD
Xét tam giác AEB ta có: AE + BE > AB (trong một tam giác tổng hai cạnh luôn lớn hơn cạnh còn lại)
Xét tam giác DEC ta có: DE + CE > DC (trong một tam giác tổng hai cạnh luôn lớn hơn cạnh còn lại)
Cộng vế với vế ta có: AE + BE + DE + CE > AB + DC
(AE + CE) + (BE + DE) > AB + DC
AC + BD > AB + DC
Tương tự ta có AC + BD > AD + BC
Kết luận: Trong một tứ giác tổng hai đường chéo luôn lớn hơn tổng hai cạnh đối.
Nửa chu vi của tứ giác ABCD là: \(\dfrac{AB+BC+CD+DA}{2}\)
Theo chứng minh trên ta có:
\(\dfrac{AB+BC+CD+DA}{2}\)< \(\dfrac{\left(AB+CD\right)\times2}{2}\) = AB + CD (1)
Vì trong một tam giác tổng hai cạnh bao giờ cũng lớn hơn cạnh còn lại nên ta có:
AB + AD > BD
AB + BC > AC
BC + CD > BD
CD + AD > AC
Cộng vế với vế ta có:
(AB + BC + CD + DA)\(\times\)2 > (BD + AC ) \(\times\) 2
⇒AB + BC + CD + DA > BD + AC (2)
Kết hợp (1) và (2) ta có:
Tổng hai đường chéo của tứ giác lớn hơn nửa chu vi của tứ giác nhưng nhỏ hơn chu vi của tứ giác
dễ lắm :)