Xác định a và b để đa thức $2 x^3-x^2+a x+b$ chia hết cho đa thức $x^2-1$.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
22 tháng 10 2019
2x^3+3x^2-x+a x^2+x-1 2x+1 2x^3+x^2 - - 2x^2-x+a 2x^2+x -2x+a -2x-1 - a+1
Để \(A\left(x\right)⋮B\left(x\right)\Leftrightarrow a+1=0\)
\(\Leftrightarrow a=-1\)
Vậy ...
LV
0
HH
2
AH
Akai Haruma
Giáo viên
30 tháng 1 2022
Lời giải:
Đặt $f(x)=ax^3+bx^2-11x+10$
$x^2+x-2=(x-1)(x+2)$
Do đó để $f(x)\vdots x^2+x-2$ thì $f(x)\vdots x-1$ và $f(x)\vdots x+2$
$\Leftrightarrow f(1)=f(-2)=0$ (theo định lý Bê-du về phép chia đa thức)
$\Leftrightarrow a+b-1=-8a+4b+32=0$
$\Leftrightarrow a=3; b=-2$
19 tháng 1 2017
Giao luu vấn đề mới
x=1, -2 là nghiệm
\(\hept{\begin{cases}a-\left(a+1\right)-\left(2b+1\right)+3b=0\\-8a-2\left(a+1\right)+2\left(2b+1\right)+3b=0\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}b=2\\-10a+7b=0\Rightarrow a=\frac{14}{10}=\frac{7}{5}\end{cases}}\)
IS
1
KN
3 tháng 11 2019
Câu hỏi của Phạm Thị Quỳnh Tú - Toán lớp 8 - Học toán với OnlineMath
Tham khảo
BM
0
FT
2
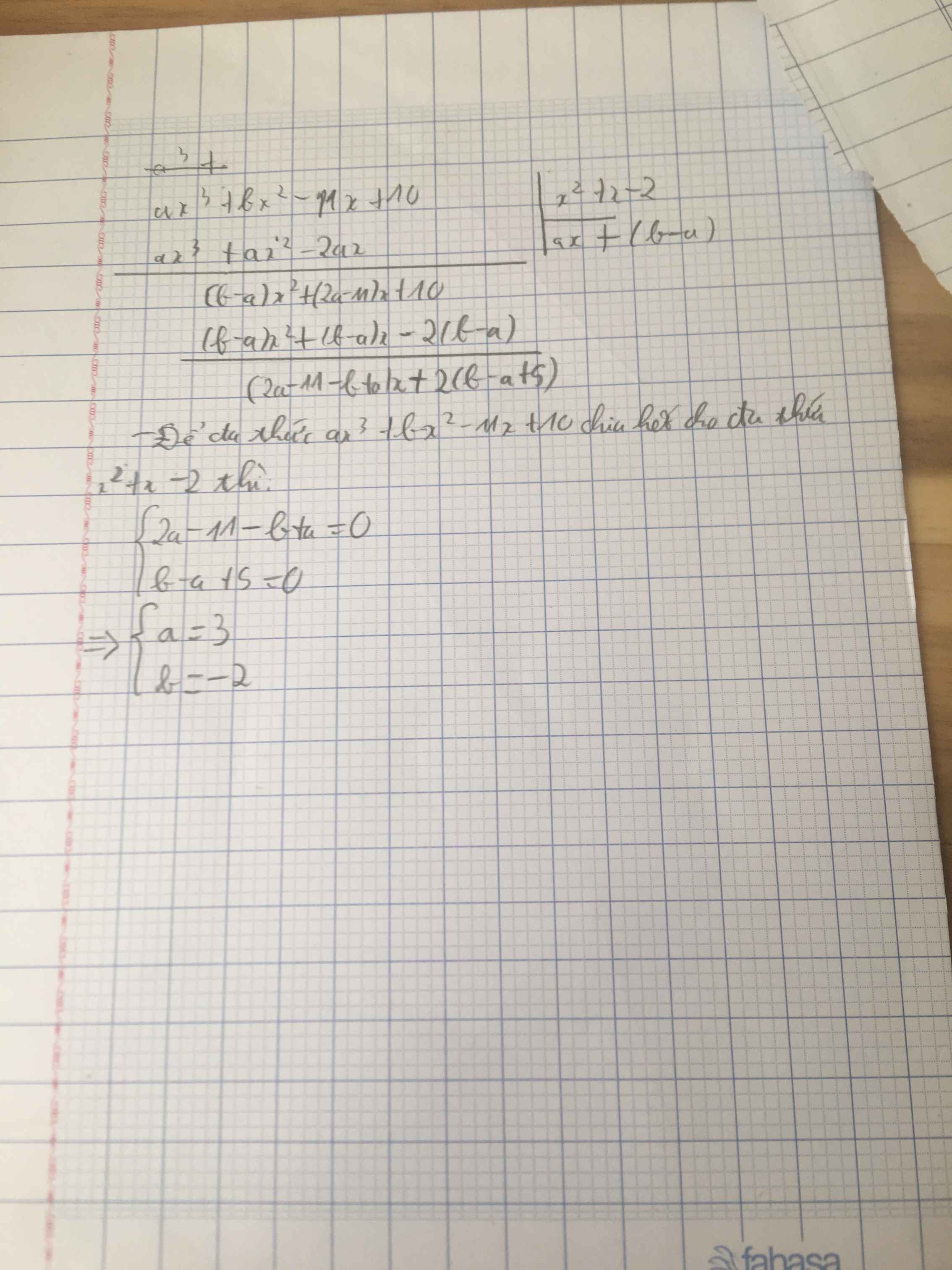
Đa thức \(2x^3-x^2+ax+b\)(*) chia hết cho \(x^2-1\) nên hai đa thức này có cùng nghiệm:
Ta có: \(x^2-1=0\Leftrightarrow x=\pm1\)
+) Do `x=1` là nghiệm nên thay \(x=1\) vào (*) thì (*) sẽ bằng 0 ta có:
\(2\cdot1^3-1^2+a\cdot1+b=0\)
\(\Leftrightarrow2-1+a+b=0\)
\(\Leftrightarrow a+b=-1\Leftrightarrow a=-1-b\) (1)
+) Do \(x=-1\) là nghiệm nên thay \(x=-1\) vào (*) thì (*) sẽ bằng 0 ta có:
\(2\cdot\left(-1\right)^3-\left(-1\right)^2+a\cdot\left(-1\right)+b=0\)
\(\Leftrightarrow-2-1-a+b=0\)
\(\Leftrightarrow b-a=3\) (2)
Thay (1) vào (2) ta có:
\(b-a=3\Leftrightarrow b-\left(-1-b\right)=3\)
\(\Leftrightarrow b+1+b=3\)
\(\Leftrightarrow2b=2\)
\(\Leftrightarrow b=1\)
\(\Rightarrow a=-1-1=-2\)
Vậy: ...