(2 điểm)
Cho tam giác $A B C$ vuông tại $A$. Tia phân giác góc $B$ cắt $A C$ tại $D$. Từ $D$ kẻ $D H$ vuông góc với $ {BC}$.
a) So sánh: $ {BA}$ và $ {BC}$.
b) Chứng minh: $ {DA}= {DH}$.
c) So sánh: $ {DC}$ và $ {DA}$.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
H9
HT.Phong (9A5)
CTVHS
6 tháng 2
Đúng(1)
H9
HT.Phong (9A5)
CTVHS
6 tháng 2
Đúng(1)
Những câu hỏi liên quan
24 tháng 4 2018
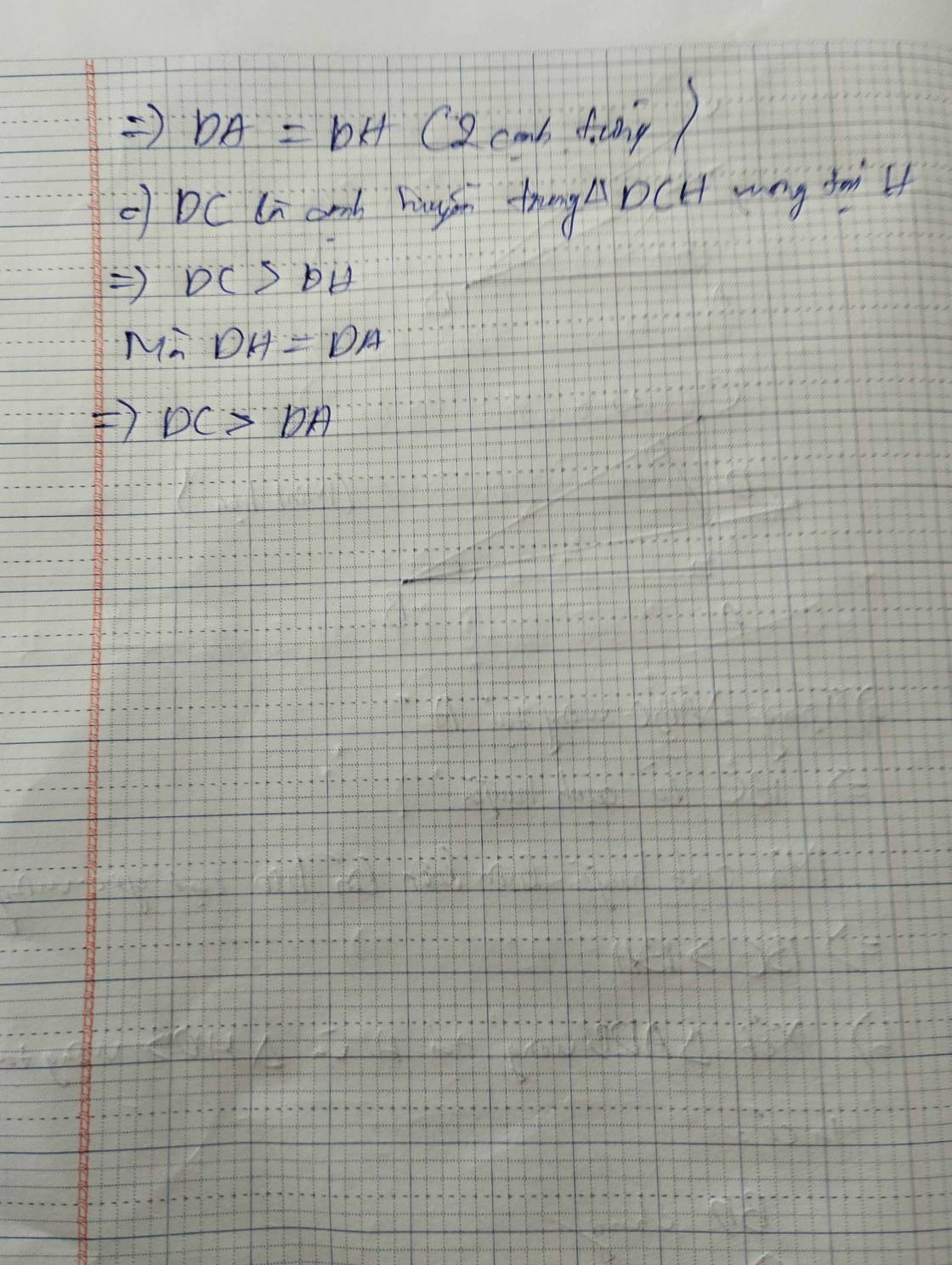
a) Xét tam giác ABD và tam giác BDH có: góc B1= góc B2 (do BĐ là pg ABD)
BD cạnh chung
góc ABD= góc BHD( =90 độ)
=> tam giác ABD= tam giác BDH( g.c.g)
=> AD=DH( 2 cạnh tương ứng)
b) mk ki bt làm
c) Xét tam giác BHK vuông tại H có: góc B+ góc HKB= 90 độ( t/c)
Xét tam giác BAC có : góc B+ góc ACB= 90 độ( t/c)
=> góc HKB= góc ACB (cùng phụ vs góc B)
=> góc AKD = góc HCD
Xét tam giác ADK và tam giác HDC có:
góc AKD = góc HCD(cmt)
AD=DH( c/m câu a)
góc KAD= góc DHC( = 90 độ)
=> tam giác ADK= tam giác HDC( g.c.g)
=> AK=HC( 2 cạnh tương ứng)
Mà BA= BH( tam giác ABD= tam giác BDH)
BA+ AK= BK , BH+HC= BC
=> BK=BC
=> tam giác KBC cân tại B( đpcm)
24 tháng 4 2018
a) Xét tam giacd ABD và tam giác HBD có :
góc ABD = góc HBD ( vì BD là tia phân giác )
BD : cạnh chung
Góc BAD = góc BHD = 90 độ
=> tam giác ABD = tam giác HBD ( cạnh huyền - góc nhọn )
=> AD = DH ( cặp cạnh tương ứng )
b) Xét tam giác HDC có :
góc DHC = 90 độ ( vì kề bù với góc BHD = 90 độ )
=> DC > DH ( vì DC là cạnh đối diện với góc vuông )
mà AD = DH ( câu a)
=> AD < DC ( đpcm )
c) Vì AB = BH ( vì tam giác ABD = tam giác HBD )
=> tam giác ABH cân
Xét tam giác ADK và tam giác HDC có
AD = DH ( vì tam fiacs ABD = tam giác HBD )
góc KAD = góc CHD = 90
Góc ADK = góc HDC ( đối đỉnh )
=> tam giác ADK = tam giác HDC ( g-c-g )
=> AK = HC ( cặp cạnh tương ứng )
mà AB + AK = BK
BH + CH = BD
Mà AB = BH (cmt )
=> BK = BC
=> tam giác KBC cân (đpcm )
28 tháng 7 2023
a: Xét ΔBAD vuông tại A và ΔBHD vuông tại H có
BD chung
góc ABD=góc HBD
=>ΔBAD=ΔBHD
=>DA=DH
b: DA=DH
DH<DC
=>DA<DC
c: Xét ΔBHK vuông tại H và ΔBAC vuông tại A có
BH=BA
góc HBK chung
=>ΔBHK=ΔBAC
=>BK=BC
=>ΔBKC cân tại B
18 tháng 5 2016
Xét tam giác ABD và tam giác HBD có:
BD: chung.
Góc BAD=BHD=90 độ.
Góc ABD=HBD(Phân giác BD)
=> Tam giác ABD=tam giác HBD(ch-gn)
b/ Gọi giao điểm của BD và AH là O.
Xét tam giác AOB và tam giác HOB có:
BO:chung.
Góc ABO=HBO(Phân giác BD)
BA-BH(cạnh tương ứng của tam giác BAD=BHD)
=>Tam giác AOB=tam giác HOB(c-g-c)
=> Góc AOB=HOB(góc tương ứng)=90 độ
Góc BAH=BKC(góc ứng với cạnh đáy của tam giác cân có cùng góc B)
=> AH//KC
Mà BD vuông góc với AH nên BD cũng vuông góc với KC.
c/Xét tam giác ADK và tam giác HDC có:
DA=DH(cạnh tương ứng của tam giác BAD=tam giác BHD)
Góc DAK=DHC=90 độ.
Góc ADK=HDC(đối đỉnh)
=> tam giác ADK=tam giác HDC(g-c-g)
=> DK=DC(cạnh tương ứng)
Mà trong tam giác vuông HDC có:
DC là cạnh huyền nên DC>DH
=> DK>DH(đpcm)
5 tháng 1 2022
a: Xét ΔBAD vuông tại A và ΔBHD vuông tại H có
BD chung
\(\widehat{ABD}=\widehat{HBD}\)
Do đó: ΔBAD=ΔBHD
Suy ra: BA=BH
b: Ta có: ΔBAD=ΔBHD
nên DA=DH
hay D nằm trên đường trung trực của AH(1)
Ta có: BA=BH
nên B nằm trên đường trung trực của AH(2)
Từ (1) và (2) suy ra BD là đường trung trực của AH
hay BD⊥AH
12 tháng 2 2022
Mình chỉ làm câu c, d thôi nha ( vì câu a, b bạn Nguyễn Lê Phước Thịnh làm rồi)
c) Xét tam giác ECK và tam giác ECA có:
EKC=EAC=90
EC cạnh chung
ECK=ECA ( vì CE là p/g của ABC)
=>Tam giác ECK=Tam giác ECA ( ch-gn)
=>CK=CA( 2 cạnh tương ứng)
Mà AB=HB( chứng minh a)
=>CK+BH=CA+AB
=>CH+KH+BK+HK=AC+AB
=>(BK+KH+CH)+HK=AC+AB
=>BC+HK=AB+AC (ĐPCM)
d) Ta có: \(\left\{{}\begin{matrix}CK=CA\left(theo.c\right)\\BA=BH\left(theo.a\right)\end{matrix}\right.\)=>Tam giác ACK cân tại C và tam giác ABH cân tại B
=>\(\left\{{}\begin{matrix}CAK=CKA=\dfrac{180-ACB}{2}\\BAH=BHA=\dfrac{180-ABC}{2}\end{matrix}\right.\)
Có: BAH+CAK=BAK+HAK+HAC+HAK=BAK+2HAK+HAC=\(\dfrac{180-ABC}{2}+\dfrac{180-ACB}{2}\)=\(\dfrac{360-\left(ABC+ACB\right)}{2}\)
=\(\dfrac{360-90}{2}=135\)
=>BAK+2HAK+HAC=135
Mà BAK+HAC=BAC-HAK=90-HAK
=>90-HAK+2HAK=135
=>90+HAK=135
=>HAK=45
3 tháng 5 2019
4 bài toàn là hình, lại khó, dài , mk nghĩ chắc ko ai tl giúp bn đâu, xl nha, ngay mk mới lp 6 cx chưa thể giải đc vì đã lp 7 đâu. ah hay là bn gửi tg bài 1 cho các bn ấy giải từ từ, cứ 1 đốg thì ai giải giúp bn đc. sorry nha
*In đậm: quan trọng.