1/2024 + 3/2024 + 5/2024 + … + 2023/2024
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NN
13 tháng 2 2023
\(A=\dfrac{2024^{2023}+1}{2024^{2024}+1}\)
\(2024A=\dfrac{2024^{2024}+2024}{2024^{2024}+1}=\dfrac{\left(2024^{2024}+1\right)+2023}{2024^{2024}+1}=\dfrac{2024^{2024}+1}{2024^{2024}+1}+\dfrac{2023}{2024^{2024}+1}=1+\dfrac{2023}{2024^{2024}+1}\)
\(B=\dfrac{2024^{2022}+1}{2024^{2023}+1}\)
\(2024B=\dfrac{2024^{2023}+2024}{2024^{2023}+1}=\dfrac{\left(2024^{2023}+1\right)+2023}{2024^{2023}+1}=\dfrac{2024^{2023}+1}{2024^{2023}+1}+\dfrac{2023}{2024^{2023}+1}=1+\dfrac{2023}{2024^{2023}+1}\)
Vì \(2024>2023=>2024^{2024}>2024^{2023}\)
\(=>2024^{2024}+1>2024^{2023}+1\)
\(=>\dfrac{2023}{2024^{2023}+1}>\dfrac{2023}{2024^{2024}+1}\)
\(=>A< B\)
\(#PaooNqoccc\)
VN
Võ Ngọc Phương
VIP
1 tháng 8 2023
a) \(2023^{2024}\) và \(2023^{2023}\)
vì 2024 > 2023 nên 20232024 > 20232023
Vậy 20232024 > 20232023
b) \(17^{2024}\) và \(18^{2024}\)
vì 17 < 18 nên 172024 < 18 2024
Vậy 172024 < 182024
NS
2
DT
0
NT
1
VH
1
ND
1
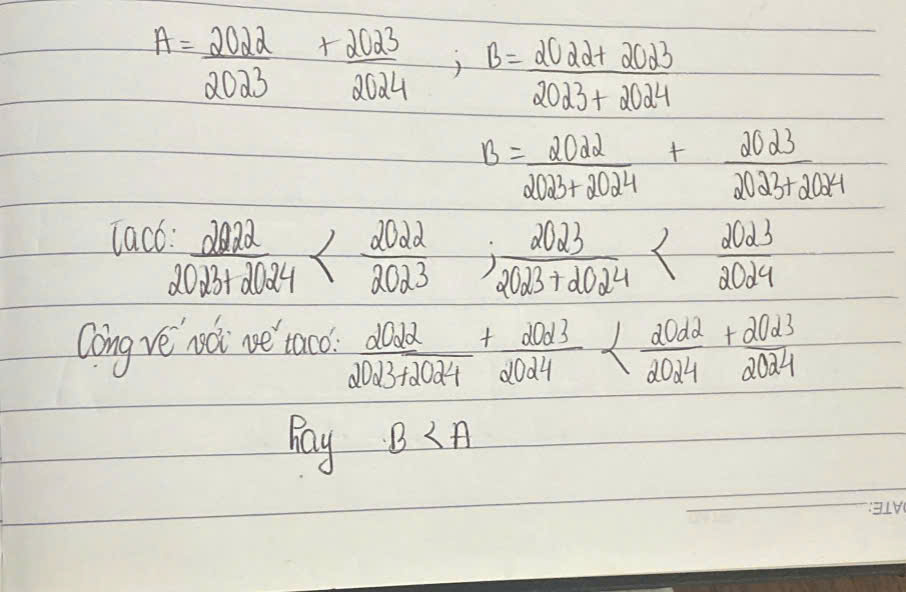
Lời giải:
$A=\frac{1}{2024}+\frac{3}{2024}+\frac{5}{2024}+...+\frac{2023}{2024}$
$=\frac{1+3+5+...+2023}{2024}$
Xét tử số:
$1+3+5+...+2023$
Số số hạng: $(2023-1):2+1=1012$
$1+3+5+...+2023=(2023+1)\times 1012:2=1024144$
$A=\frac{1024144}{2024}=506$
Đặt \(A=\dfrac{1}{2024}+\dfrac{3}{2024}+\dfrac{5}{2024}+...+\dfrac{2023}{2024}\)
\(A=\dfrac{1+3+5+...+2023}{2024}\)
Nhận xét tử số:
\(1+3+5+...+2023\)
Số số hạng của tử số trên:
\(\left(2023-1\right):2+1=1012\)(số hạng)
Tổng của tử số:
\(\left(2023+1\right)\times1012:2=1024144\)
Vậy \(1+3+5+...+2023=\left(2023+1\right)\times1012:2=1024144\).
Vậy ta có: \(A=\dfrac{1024144}{2024}=506\)
Vậy \(\dfrac{1}{2024}+\dfrac{3}{2024}+\dfrac{5}{2024}+...+\dfrac{2023}{2024}=506\)