Giúp em bài này với ạ (chi tiết+hình)
K
Khách
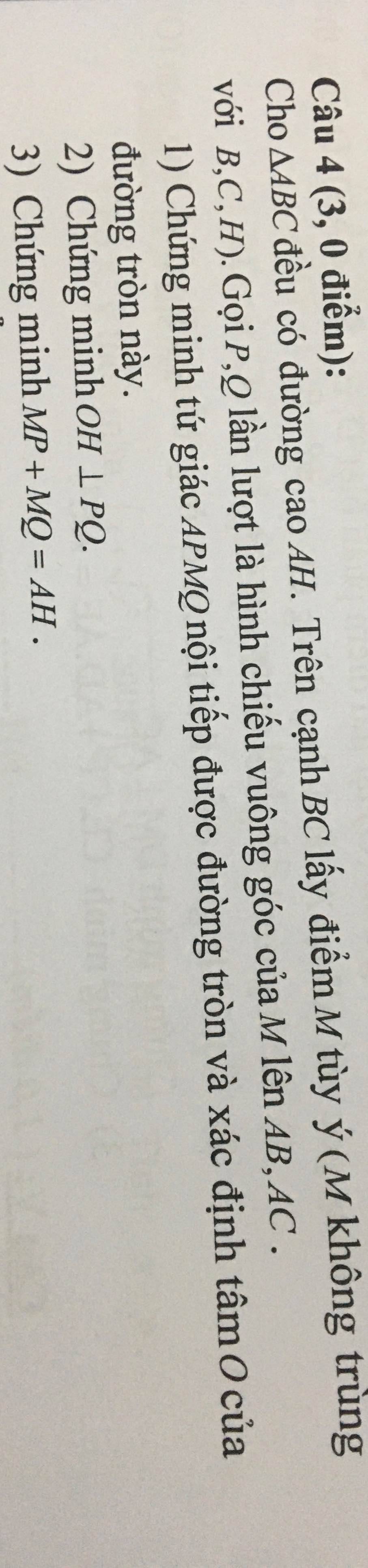
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
2
TP
3 tháng 8 2021
\(\dfrac{2A}{2A+16.5}=\dfrac{43,66}{100}\)
=> \(200A=43,66.\left(2A+16.5\right)\)
=> \(200A-87,32A=3492,8\)
=> \(112,68A=3492,8\)
=> A= 31
HN
1
HP
19 tháng 12 2021
\(\left\{{}\begin{matrix}6u_2+u_5=1\\3u_3+2u_4=-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}6u_1.q+u_1.q^4=1\\3u_1.q^2+2u_1.q^3=-1\end{matrix}\right.\)
\(\Rightarrow u_1\left(6q+q^4+3q^2+2q^3\right)=0\)
\(\Leftrightarrow q^3+2q^2+3q+6=0\)
\(\Leftrightarrow\left(q+2\right)\left(q^2+3\right)=0\)
\(\Leftrightarrow q=-\text{}2\)
\(\Rightarrow u_1=\dfrac{1}{4}\)
\(\Rightarrow u_n=u_1.q^{n-1}=\dfrac{1}{4}.\left(-2\right)^{n-1}=\left(-2\right)^{n-3}\)
11 tháng 4 2023
Gọi độ dài AB và vận tốc dự kiến lần lượt là x,y
Theo đề, ta có hệ:
\(\left\{{}\begin{matrix}\dfrac{x}{y}=\dfrac{10}{3}\\\dfrac{x}{y+5}=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x-10y=0\\x-3y=15\end{matrix}\right.\)
=>x=150 và y=45
giúp em bài này với ạ,giải chi tiết luôn nha,em cảm ơn
16 tháng 12 2021
\(x=\left(\dfrac{1}{2}\right)^3:\left(\dfrac{1}{2}\right)=\left(\dfrac{1}{2}\right)^{3-1}=\left(\dfrac{1}{2}\right)^2=\dfrac{1}{4}\)
LT
0
AN
1
2
22 tháng 5 2023
Ptr có `2` nghiệm phân biệt `<=>\Delta' > 0`
`=>(m+1)^2-m^2+2m-3 > 0`
`<=>m^2+2m+1-m^2+2m-3 > 0`
`<=>m > 1/2`
`=>` Áp dụng Viét có: `{(x_1+x_2=-b/a=2m+2),(x_1.x_2=c/a=m^2-2m+3):}`
Ta có: `1/[x_1 ^2]-[4x_2]/[x_1]+3x_2 ^2=0`
`=>1-4x_1.x_2+3(x_1.x_2)^2=0`
`<=>1-4(m^2-2m+3)+3(m^2-2m+3)^2=0`
`<=>[(m^2-2m+3=1),(m^2-2m+3=1/3):}`
`<=>[(m^2-2m+2=0(VN)),(m^2-2m+8/3=0(VN)):}`
`=>` Không có `m` thỏa mãn.
LM
ai giải giúp em mấy bài toán này vs ạ giải chi tiết giúp em ạ
2
10 tháng 11 2021
\(1,\\ a,=6x^4y^4-x^3y^3+\dfrac{1}{2}x^4y^2\\ b,=4x^3+5x^2-8x^2-10x+12x+15\\ =4x^3-3x^2+2x+15\\ 2,\\ a,=7\left(x^2-6x+9\right)=7\left(x-3\right)^2\\ b,=\left(x-y\right)^2-36=\left(x-y-6\right)\left(x-y+6\right)\\ 3,\\ \Leftrightarrow x\left(x^2-0,36\right)=0\\ \Leftrightarrow x\left(x-0,6\right)\left(x+0,6\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=0,6\\x=-0,6\end{matrix}\right.\)
NA
Nguyễn An Ninh
VIP
3 tháng 5 2023
=4090506-\(\dfrac{3}{2023}\)*2021+2020
=4090506-\(\dfrac{6063}{2023}\)+2020
=\(\dfrac{8279174035}{2023}\) tối giản luôn rồi nhé
26 tháng 8 2021
\(M=\dfrac{\sqrt{x}+3}{\sqrt{x}-3}\left(đk:x\ge0,x\ne9\right)\)
Để \(M=\dfrac{\sqrt{x}+3}{\sqrt{x}-3}< 0\) thì
\(\sqrt{x}-3< 0\) ( do \(\sqrt{x}+3\ge3>0\))
\(\Leftrightarrow\sqrt{x}< 3\Leftrightarrow0\le x< 9\)
Mà \(x\in Z\)
\(\Rightarrow x\in\left\{0;1;2;3;4;5;6;7;8\right\}\)
a: Xét tứ giác APMQ có \(\widehat{APM}+\widehat{AQM}=90^0+90^0=180^0\)
nên APMQ là tứ giác nội tiếp đường tròn đường kính AM
Tâm O là trung điểm của AM
b: Ta có: ΔAHM vuông tại H
=>H nằm trên đường tròn đường kính AM
=>H nằm trên (O)
Ta có: ΔABC đều
mà AH là đường cao
nên AH là phân giác của góc BAC
Xét (O) có
\(\widehat{PAH}\) là góc nội tiếp chắn cung PH
\(\widehat{QAH}\) là góc nội tiếp chắn cung QH
\(\widehat{PAH}=\widehat{QAH}\left(cmt\right)\)
Do đó: \(sđ\stackrel\frown{HP}=sđ\stackrel\frown{HQ}\)
Xét (O) có
\(\widehat{QPH}\) là góc nội tiếp chắn cung QH
\(\widehat{HQP}\) là góc nội tiếp chắn cung HP
\(sđ\stackrel\frown{QH}=sđ\stackrel\frown{HP}\)
Do đó: \(\widehat{HPQ}=\widehat{HQP}\)
=>HQ=HP
=>H nằm trên đường trung trực của QP(1)
Ta có: OP=OQ
=>O nằm trên đường trung trực của QP(2)
Từ (1) và (2) suy ra HO là đường trung trực của PQ
=>HO\(\perp\)PQ