Cho tam giác ABC có góc A bằng 90 độ. AH vuông góc với BC. Phân giác BD cắt AH tại I.
a) Chứng minh tam giác AID cân
b) AD.BD=BI.DC
c) Kẻ DK vuông góc với BC. Tứ giác AKDI là hình gì? Chứng minh
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HN
9 tháng 5 2022
a. Xét Δ ABE và Δ KBE có:
^B1=^B2(BD là tia p/g)
^BEA=^KEB=90o
AE chung
=> ΔABE=ΔKBE(g.c.g)
=>AB=KB
=>ΔABK cân tại B
(xin lỗi mình ko biết phần b,c,d) ;-;
cho bạn cái hình nè :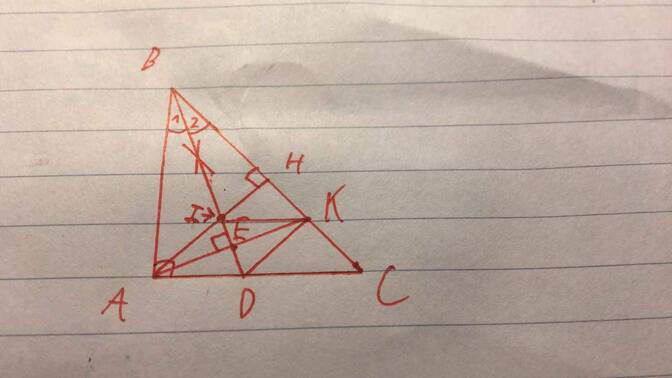
23 tháng 5 2023
a) Ta có $\angle ABD = \angle EBD$ (vì BD là phân giác của góc $\angle ABC$), và $\angle ADB = \angle EDB = 90^\circ$ (vì DE vuông góc với BC). Vậy tam giác ABD và tam giác EBD có cặp góc đồng nhất, nên chúng bằng nhau theo trường hợp góc - góc - góc của các tam giác đồng dạng. Do đó, ta có tam giác ABD = tam giác EBD.
b) Ta cần chứng minh AH song song với DE, và tam giác AID cân.
Ta có $\angle ABD = \angle EBD$ (theo phần a)), và $\angle ADB = \angle EDB = 90^\circ$ (vì DE vuông góc với BC). Vậy tam giác ABD và tam giác EBD đồng dạng. Do đó:
$$\frac{AB}{EB} = \frac{BD}{BD} = 1$$
$$\Rightarrow AB = EB$$
Mà $AH$ là đường cao của tam giác $ABC$, nên $AB = AH \cos(\widehat{BAC})$. Tương tự, ta có $EB = ED \cos(\widehat{BAC})$. Vậy:
$$\frac{AH}{ED} = \frac{AB}{EB} = 1$$
Do đó, $AH = ED$, hay $AH$ song song với $DE$.
Tiếp theo, ta chứng minh tam giác $AID$ cân. Ta có:
$$\angle AID = \angle BID - \angle BIA = \frac{1}{2} \angle ABC - \angle BAC$$
Mà $\angle ABC = 90^\circ + \angle BAC$, nên:
$$\angle AID = \frac{1}{2}(90^\circ + \angle BAC) - \angle BAC = \frac{1}{2}(90^\circ - \angle BAC)$$
Tương tự, ta có:
$$\angle ADI = \frac{1}{2} \angle ADB = \frac{1}{2} \cdot 90^\circ = 45^\circ$$
Vậy tam giác $AID$ có hai góc bằng nhau là $\angle AID$ và $\angle ADI$, nên đó là tam giác cân.
Vậy, ta đã chứng minh được rằng $AH$ song song với $DE$, và tam giác $AID$ cân.
23 tháng 5 2023
Xem lại KHỐI LỚP và cách áp dụng KIẾN THỨC như thế nào cho đúng với lứa tuổi.
các bạn ơi giúp mình phần c với vì mik sắp phải nộp bài rồi .cảm ơn các bạn rất nhiều.
a,
Xét \(\Delta AIB\)và \(CDB\)có :
\(+,\widehat{ABI}=\widehat{DBC}\)( Do \(BD\)là phân giác )
\(+,\widehat{BAI}=\widehat{BCD}\)( cùng phụ \(\widehat{ABC}\))
Vậy tam giác \(AIB~CDB\left(g.g\right)\)
Suy ra : \(\frac{CD}{BC}=\frac{AI}{AB}\)
Mà theo tính chất phân giác \(\frac{CD}{BC}=\frac{AD}{AB}\Rightarrow AD=AI\)hay \(AID\)cân tại \(A\)
b,
Tam giác \(ABI~CBD\)
Suy ra : \(\frac{BI}{BD}=\frac{AI}{CD}=\frac{AD}{CD}\)
\(\Rightarrow BI.CD=AD.BD\)
c,
Dễ dàng chứng minh tam giác \(ADB=KDB\Rightarrow AD=DK\Rightarrow AI=DK\)
Lại có AI // DK ( cùng vuông góc BC )
Vậy \(AIKB\)là hình bình hành do 2 cạnh đối song song và bằng nhau.
Lại có \(AI=AD\)nên \(AIKB\)là hình thoi.