Chứng minh rằng nếu trung tuyến AM của tam giác ABC bé hơn nửa đọ dài cạnh BC thì góc A phải là góc tù.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NT
nguyễn thị hương giang
31 tháng 1
Đúng(1)
Những câu hỏi liên quan
3 tháng 2 2022
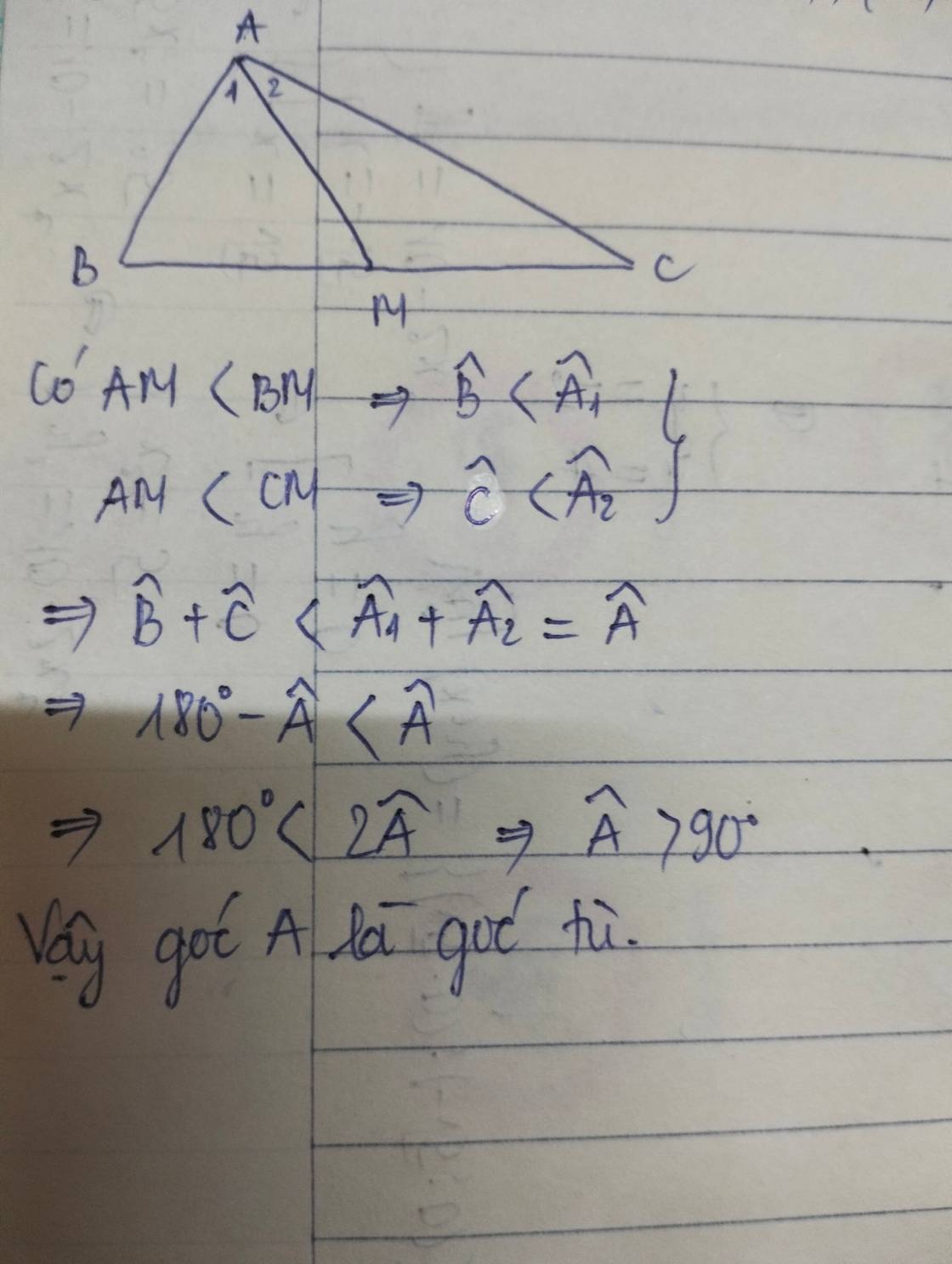
Xét ΔABC có
AM là đường trung tuyến
AM là đường cao
Do đó: ΔABC cân tại A
CM
25 tháng 10 2017
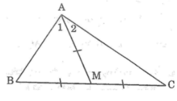
Vì AM là đường trung tuyến của ΔABC nên BM = MC = 1/2 BC
Mà AM = 1/2 BC (gt) nên: AM = BM = MC.
Tam giác AMB có AM = MB nên ΔAMB cân tại M
Suy ra: ∠B = ∠A1 (tính chất tam giác cân) (1)
Tam giác AMC có AM = MC nên ΔAMC cân tại M
Suy ra: ∠C = ∠A2 (tính chất tam giác cân) (2)
Từ (1) và (2) suy ra: ∠B + ∠C = ∠A1 + ∠A2 = ∠(BAC) (3)
Trong ΔABC ta có:
∠B + ∠C + ∠(BAC) = 180o (tổng ba góc trong tam giác) (4)
Từ (3) và (4) suy ra: ∠(BAC) + ∠(BAC) = 180o ⇔ 2∠(BAC) = 180o
Hay ∠(BAC) = 90o.
Vậy ΔABC vuông tại A.
26 tháng 2 2015
1/Giả sử trong 1 tam giác có 2 hóc tù thì tổng 3 góc của tam giác đó sẽ lớn hơn 180 độ
=>trong 1 tam giác chỉ có duy nhất 1 góc tù
2/Trong 1 tam giác nếu góc nhỏ nhất bằng 60 độ thì tổng 3 góc của tam giác đó sẽ lớn hơn 180 độ
=> trong một tam giác góc nhỏ nhất không thể lớn hơn 60 độ
3/Xét tam giác AMB = tam giác AMC (c.c.c)
=> góc BMA = góc CMA
Mặt khác góc BMA + góc CMA = 180 độ
=> góc BMA = góc CMA = 90 độ
=> AM vuông góc BC
=> AM là đường cao của tam giác hạ từ đỉnh A
Tam giác BMA = tam giác CMA
=> góc BAM = góc CAM
=> AM là tia phân giác của góc A
N
2
3 tháng 4 2016
ta có AM=1/2BC,mà BM=CM=1/2BC
=> AM=BM=CM
ta có BM=AM=> tam giác AMB cân tại M=> góc A1= góc B
ta có AM=MC=>tam giác AMC cân tại M=> góc A2=góc C
tam giác ABC có góc B+A1+A2+C=180 độ
=> A1+A1+A2+A2=180 độ
=> 2(A1+A2)=180 độ
=> A1+A2=90độ
vậy góc BAC=90 độ
3 tháng 4 2016
giải: vò MA = MB (gt)
=> tam giác AMB cân tại M
=> góc B = góc A1 ( đ/lý) (1)
MA = MC (gt)
=> tam giác AMC cân tại M
=> góc C = góc A2 (đ/lý) (2)
trong tam giác ABC có: góc A + góc B + góc C = 1800 (đ/lý)
hay góc A1 + A2 + góc B + góc C = 1800 (3)
từ (1), (2) , (3) => 2 góc A1 + 2 góc A2 = 1800
2 ( góc A1 + góc A2) = 1800
góc A1 + góc A2 = 900
hay góc BAC = 900
BM
0