Một quân mã cần di chuyển từ A đến B trên bàn cờ vua \(8\times8\). Chứng minh rằng với mọi vị trí tùy ý của A và B, luôn có cách để quân mã thực hiện hành trình với ít hơn hoặc bằng 6 bước.

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

| a | b | c | d | e | |
| 5 | |||||
| 4 | |||||
| 3 | |||||
| 2 | |||||
| 1 |
Ta đánh dấu bảng 5x5 như trên và không mất tính tổng quát, giả sử quân mã ban đầu ở vị trí a1. Khi đó một đường đi của quân mã để đi hết tất cả các ô trên bàn cờ (với điều kiện mỗi ô chỉ được đi qua 1 lần) là:
a1-c2-e1-d3-e5-c4-a5-b3-c1-e2-d4-b5-a3-b1-d2-e4-c5-a4-b2-d1-e3-d5-b4-a2-c3.
cái này đúng rồi á chị nhưng mà nhìn bàn cờ nó cũng cứ kiểu gì ấy....
Hì hì...

Vị trí của quân xe: hàng 3, cột c
Vị trí của quân mã: hàng 5, cột f

Đáp án D
Phương pháp :
Quân vua được di chuyển sang một ô khác chung cạnh hoặc chung đỉnh với ô đang đứng => | Ω |
Gọi A là biến cố : « Quân vua sau 3 bước trở về đúng vị trí ban đầu » . Tính |A| .
Cách giải :
Quân vua được di chuyển sang một ô khác chung cạnh hoặc chung đỉnh với ô đang đứng => | Ω | = 8 3 .
Gọi A là biến cố : « Quân vua sau 3 bước trở về đúng vị trí ban đầu »
TH1: Quân vua di chuyển bước thứ nhất sang ô đen liền kề (được tô màu đỏ) có 4
cách.
Bước đi thứ 2 quân vua di chuyển sang các ô được tô màu vàng có 4 cách.
Bước đi thứ 3 quay về vị trí ban đầu có 1 cách.
Vậy TH này có 4.4 = 16 cách.
TH2: Quân vua di chuyển bước thứ nhất sang các ô trắng liền kề (được tô màu đỏ) có
4 cách.
Bước đi thứ 2 quân vua di chuyển sang các ô được tô màu vàng có 2 cách.
Bước đi thứ 3 quay về vị trí ban đầu có 1 cách.
Vậy TH này có 4.2 = 8 cách
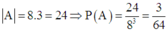

Chọn A
Không gian mẫu là 8 3
Có hai trường hợp
+ Trường hợp 1: Bước 1 đi 4 ô góc thì bước 2 có 2 cách đi, bước 3 có 1 cách đi
+ Trường hợp 2: Bước 1 đi 4 ô còn lại thì bước 2 có 4 cách đi, bước 3 có 1 cách đi
Vậy tât cả có 4.2 + 4.4 = 24
Suy ra xác suất để sau 3 bước đi quân vua trở về ô ban đầu là: 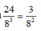
Chơi cờ thoai cơ mà áp lực ngang zậy đó -)