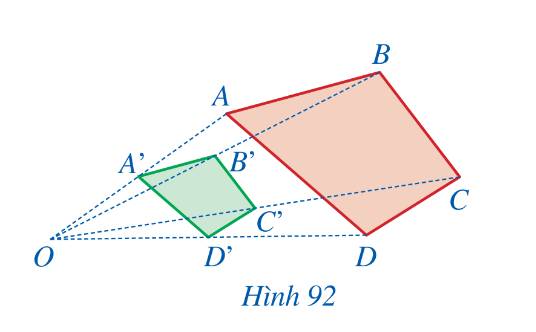
Cho hai tứ giác ABCD và A’B’C’D’ sao cho bốn đường thẳng AA’, BB’, CC’, DD’ cùng đi qua điểm O và \(\dfrac{OA'}{OA}=\dfrac{OB'}{OB}=\dfrac{OC'}{OC}=\dfrac{OD'}{OD}=\dfrac{1}{2}\) (Hình 92). Tứ giác A’B’C’D’ có thể nhận được từ tứ giác ABCD bằng cách nào?

 .
.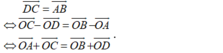
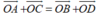
Từ điểm O, ‘‘thu nhỏ’’ hai lần tứ giác ABCD, ta sẽ nhận được tứ giác A’B’C’D’.