A=\(\dfrac{6}{3}\)+\(\dfrac{6}{15}\)+\(\dfrac{6}{35}\)+...+\(\dfrac{6}{9999}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a: \(=\left(\dfrac{3}{17}+\dfrac{14}{17}\right)+\left(\dfrac{-5}{13}-\dfrac{8}{13}\right)+\left(\dfrac{-18}{35}-\dfrac{17}{35}\right)\)
=1-1-1
=-1
b: \(=\dfrac{-3}{8}\left(\dfrac{1}{6}+\dfrac{5}{6}\right)+\dfrac{-5}{8}=\dfrac{-3}{8}-\dfrac{5}{8}=-1\)
c: \(=\dfrac{4}{4}\cdot\dfrac{5}{15}\cdot\dfrac{11}{11}=\dfrac{1}{3}\)
a)\(=\left(-\dfrac{5}{13}+\dfrac{-8}{13}\right)+\left(-\dfrac{18}{35}-\dfrac{17}{35}\right)+\left(\dfrac{3}{14}+\dfrac{14}{17}\right)=-1-1+1=-1\)
b)\(=\dfrac{-3}{8}.\left(\dfrac{1}{6}+\dfrac{5}{6}\right)-\dfrac{10}{16}=-\dfrac{3}{8}.1-\dfrac{10}{16}=-\dfrac{6}{16}-\dfrac{10}{16}=-\dfrac{16}{16}=-1\)
c)\(\dfrac{-4.5.11}{11.5.3.-4}=\dfrac{1}{3}\)

a: \(M=\dfrac{6}{5}+\dfrac{3}{2}\left(\dfrac{2}{5\cdot7}+...+\dfrac{2}{97\cdot99}+\dfrac{2}{99\cdot101}\right)\)
\(=\dfrac{6}{5}+\dfrac{3}{2}\left(\dfrac{1}{5}-\dfrac{1}{101}\right)\)
\(=\dfrac{6}{5}+\dfrac{3}{10}-\dfrac{3}{202}=\dfrac{150}{101}\)
b: 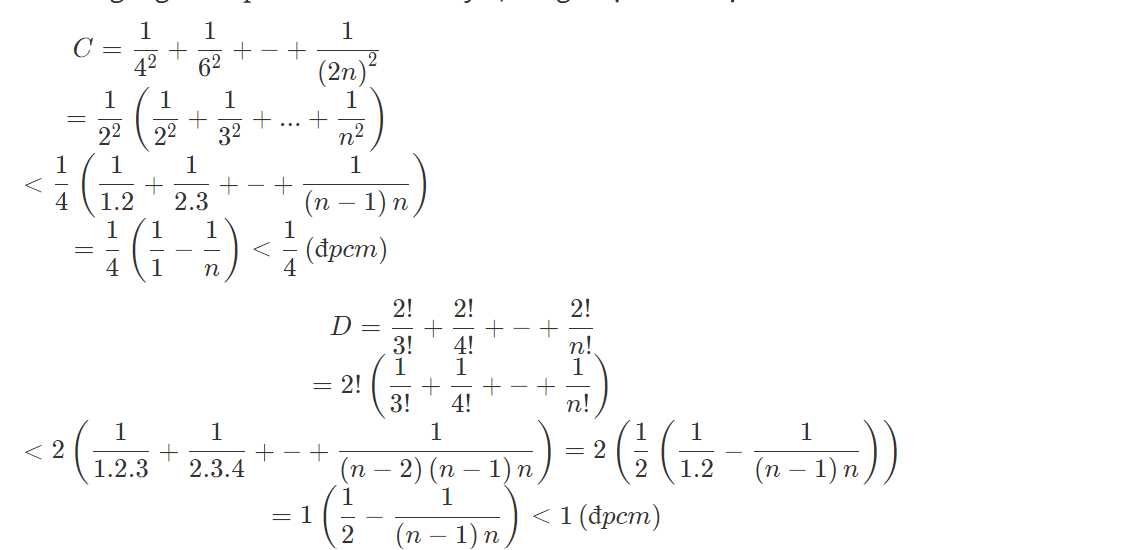

a=78/35
b=22/12
c=1/1
d=40202090/4040090
e=1,24025667172...
f=871,82
ko biết đúng ko [0_0'] hihi

\(\dfrac{2}{3}+\dfrac{5}{6}+\dfrac{9}{10}+\dfrac{14}{15}+\dfrac{20}{21}+\dfrac{27}{28}+\dfrac{35}{36}+\dfrac{44}{45}\\ =\left(1-\dfrac{1}{3}\right)+\left(1-\dfrac{1}{6}\right)+\left(1-\dfrac{1}{10}\right)+\left(1-\dfrac{1}{15}\right)+\left(1-\dfrac{1}{21}\right)+\left(1-\dfrac{1}{28}\right)+\left(1-\dfrac{1}{36}\right)+\left(1-\dfrac{1}{45}\right)\\ =8-\left(\dfrac{1}{3}+\dfrac{1}{6}+\dfrac{1}{10}+\dfrac{1}{15}+\dfrac{1}{21}+\dfrac{1}{28}+\dfrac{1}{36}+\dfrac{1}{45}\right)\\ =8-\left(\dfrac{2}{6}+\dfrac{2}{12}+\dfrac{2}{20}+\dfrac{2}{30}+\dfrac{2}{42}+\dfrac{2}{56}+\dfrac{1}{72}+\dfrac{1}{90}\right)\\ =8-\left(\dfrac{2}{2.3}+\dfrac{2}{3.4}+\dfrac{2}{4.5}+\dfrac{2}{5.6}+\dfrac{2}{6.7}+\dfrac{2}{7.8}+\dfrac{2}{8.9}+\dfrac{2}{9.10}\right)\\ =8-2\left(\dfrac{1}{2.3}+\dfrac{1}{3.4}+\dfrac{1}{4.5}+\dfrac{1}{5.6}+\dfrac{1}{6.7}+\dfrac{1}{7.8}+\dfrac{1}{8.9}+\dfrac{1}{9.10}\right)\\ =8-2\left(\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{8}+\dfrac{1}{8}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{10}\right)\\ =8-2\left(\dfrac{1}{2}-\dfrac{1}{10}\right)=8-2.\dfrac{2}{5}=8-\dfrac{4}{5}=\dfrac{36}{5}\)

TL
\(\frac{3}{15}\)-\(\frac{5}{35}\)=\(\frac{1}{5}\)\(-\frac{1}{7}\)=\(\frac{2}{35}\)
\(\frac{18}{27}\)-\(\frac{2}{6}\)=\(\frac{2}{3}\)-\(\frac{1}{3}\)=\(\frac{1}{3}\)
nha bn
HT
\(A=\dfrac{6}{3}+\dfrac{6}{15}+\dfrac{6}{35}+...+\dfrac{6}{9999}\)
\(=3\left(\dfrac{2}{3}+\dfrac{2}{15}+...+\dfrac{2}{9999}\right)\)
\(=3\left(\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+...+\dfrac{2}{99\cdot101}\right)\)
\(=3\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{99}-\dfrac{1}{101}\right)\)
\(=3\left(1-\dfrac{1}{101}\right)=3\cdot\dfrac{100}{101}=\dfrac{300}{101}\)
ai biết làm giúp mình với