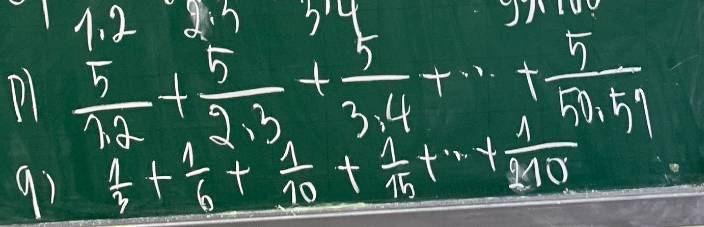
giúp em phần này gấp ạ, xin cảm ơn ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 7 2021
1. English is more interesting than music.
2. Today they are not as happy as they were yesterday.
3. Ha Noi is not as small as Hai Duong.
4. Mai's sister is not as pretty as her.
6. You have got more money than me.
7. Art is not as difficult as French.
8. Nam's father is more careful than him.
9. No one in our town is as rich as Mr Ron.
10. He is the most intelligent in my class.
11. Everest is the highest mountain in the world.
12. Minh is the fattest person in my group.
13. I can't swim as far as Jan.
14B 15C 16A 17C 18B 19C 20B
NL
0
TM
0
VD
29 tháng 5 2022
Hướng dẫn: A đạt GTLN khi \(\dfrac{1}{A}\) đạt GTNN
Ta có: \(x^2+2\ge0\forall x\)
\(\Rightarrow A=\dfrac{1}{x^2+2}\le\dfrac{1}{2}\forall x\)
Vậy GTLN của A là 1/2
=> A
TT
1
25 tháng 3 2023
1: vecto AC=(-1;-7)
=>VTPT là (-7;1)
PTTS là:
x=3-t và y=6-7t
Phương trình AC là:
-7(x-3)+1(y-6)=0
=>-7x+21+y-6=0
=>-7x+y+15=0
2: Tọa độ M là:
x=(3+2)/2=2,5 và y=(6-1)/2=2,5
PTTQ đường trung trực của AC là:
-7(x-2,5)+1(y-2,5)=0
=>-7x+17,5+y-2,5=0
=>-7x+y+15=0
3: \(AB=\sqrt{\left(-1-3\right)^2+\left(3-6\right)^2}=5\)
Phương trình (A) là:
(x-3)^2+(y-6)^2=AB^2=25
12 tháng 10 2021
a) Do mắc song song nên:
\(U_{23}=U_3=U_2=I_2.R_2=0,5.6=3\left(V\right)\)
Cường độ dòng điện I3:
\(I_3=\dfrac{U_3}{R_3}=\dfrac{3}{9}=\dfrac{1}{3}\left(A\right)\)
Do mắc nối tiếp nên:
\(I=I_1=I_{23}=I_2+I_3=0,5+\dfrac{1}{3}=\dfrac{5}{6}\left(A\right)\)
b) \(R_{23}=\dfrac{R_2.R_3}{R_2+R_3}=\dfrac{6.9}{6+9}=3,6\left(\Omega\right)\)
\(R_{AB}=R_{23}+R_1=12+3,6=15,6\left(\Omega\right)\)
Hiệu điện thế U giữa 2 đầu đoạn mạch:
\(U=I.R_{tđ}=\dfrac{5}{6}.15,6=13\left(V\right)\)
p: \(\dfrac{5}{1\cdot2}+\dfrac{5}{2\cdot3}+...+\dfrac{5}{50\cdot51}\)
\(=5\left(\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+...+\dfrac{1}{50\cdot51}\right)\)
\(=5\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{50}-\dfrac{1}{51}\right)\)
\(=5\cdot\left(1-\dfrac{1}{51}\right)=5\cdot\dfrac{50}{51}=\dfrac{250}{51}\)
q: \(\dfrac{1}{3}+\dfrac{1}{6}+\dfrac{1}{10}+...+\dfrac{1}{210}\)
\(=\dfrac{2}{6}+\dfrac{2}{12}+\dfrac{2}{20}+...+\dfrac{2}{420}\)
\(=2\left(\dfrac{1}{6}+\dfrac{1}{12}+\dfrac{1}{20}+...+\dfrac{1}{420}\right)\)
\(=2\left(\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+...+\dfrac{1}{20\cdot21}\right)\)
\(=2\left(\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{20}-\dfrac{1}{21}\right)\)
\(=2\left(\dfrac{1}{2}-\dfrac{1}{21}\right)=2\cdot\dfrac{19}{42}=\dfrac{19}{21}\)