2 quả cầu a,b co trọng lượng = nhau nhưng làm = 2 chất khác nhau được treo vào đầu của 1 đòn cứng có trọng lượng không đáng kể và có độ dài 80cm.Lúc đầu đòn cân bằng sau đó nhúng cả hai quả cầu ngập trong nước .Người ta thấy phải dịch chuyển điểm tựa đi 1 đoạn 6x cm về phía điểm b để đòn bẩy cân bằng .Tính x nếu trọng lượng riêng của quả cầu a,b lần lượt là 3.10^4N/m^3,9.10^4N/m^3và trọng lượng riêng của nước là 10^4N/m^3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan

LT
3 tháng 8 2017
Đáp án C.
Góc hợp giữa một dây treo và phương thẳng đứng là tan β = F P .

VT
28 tháng 2 2019
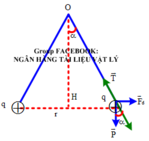
Các lực tác dụng lên vật
+ Trọng lực P → (thẳng đứng hướng xuống)
+ Lực điện F → d (hai điện tích giống nhau nên hai điện tích đẩy nhau)
+ Lực căng T →
+ Khi quả cầu cân bằng ta có: T → + F → + P → = 0
+ Từ hình vẽ ta có: tan α = F P
Chọn đáp án C
Khi hai vật treo ngoài không khí ta có cân bằng lực:
\(P_1\cdot l_1=P_2\cdot l_2\Rightarrow l_1=l_2=\dfrac{l}{2}=\dfrac{80}{2}=40\left(cm\right)\)
Nhúng cả hai quả cầu ngập trong nước ta có:
\(\left(P_1-F_{A_1}\right)\cdot l_1'=\left(P_2-F_{A_2}\right)\cdot l_2'\)
Trong đó: \(\left\{{}\begin{matrix}l_1'=l_1+6x\left(cm\right)\\l_2'=l_2-6x\left(cm\right)\end{matrix}\right.\) và \(\left\{{}\begin{matrix}F_{A_1}=V_1\cdot d_0=\dfrac{P_1}{d_1}\cdot d_0\\F_{A_2}=V_2\cdot d_0=\dfrac{P_2}{d_2}\cdot d_0\end{matrix}\right.\)
Khi đó: \(\left(P_1-\dfrac{P_1}{d_1}\cdot d_0\right)\left(l_1+6x\right)=\left(P_2-\dfrac{P_2}{d_2}\cdot d_0\right)\left(l_2-6x\right)\)
\(\Rightarrow P_1\cdot l_1+P_1\cdot6x-\dfrac{P_1}{d_1}\cdot d_0\cdot l_1-\dfrac{P_1}{d_1}\cdot d_0\cdot6x=P_2\cdot l_2-P_2\cdot6x-\dfrac{P_2}{d_2}\cdot d_0\cdot l_2+\dfrac{P_2}{d_2}\cdot d_0\cdot6x\)
Mà \(\left\{{}\begin{matrix}P_1=P_2\\l_1=l_2=40cm=0,4m\end{matrix}\right.\)
Khi đó: \(6x-\dfrac{d_0\cdot l_1}{d_1}-\dfrac{6x\cdot d_0}{d_1}=-6x-\dfrac{d_0\cdot l_2}{d_2}+\dfrac{6x\cdot d_0}{d_2}\)
\(\Rightarrow6x-\dfrac{10^4\cdot0,4}{3\cdot10^4}-\dfrac{6x\cdot10^4}{3\cdot10^4}=-6x-\dfrac{10^4\cdot0,4}{3,9\cdot10^4}+\dfrac{6x\cdot10^4}{3,9\cdot10^4}\)
\(\Rightarrow x=\dfrac{1}{275}\left(m\right)\approx0,36\left(cm\right)\)
giúp tui đi mn gấp lắm