\(\sqrt{\dfrac{3\sqrt{5}-1}{2\sqrt{5}+3}}-\sqrt{\dfrac{\sqrt{5}+11}{7-2\sqrt{5}}}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 8 2021
Bài 1:
\(D=\dfrac{1}{2}\sqrt{48}-\dfrac{\sqrt{33}}{\sqrt{11}}+5\sqrt{1\dfrac{1}{3}}=\dfrac{1}{2}.4\sqrt{3}-\sqrt{3}+5.\dfrac{2\sqrt{3}}{3}=2\sqrt{3}-\sqrt{3}+\dfrac{10\sqrt{3}}{3}=\dfrac{3\sqrt{3}+10\sqrt{3}}{3}=\dfrac{13\sqrt{3}}{3}\)
\(E=\sqrt{\dfrac{3-\sqrt{5}}{3+\sqrt{5}}}-\sqrt{\dfrac{3+\sqrt{5}}{3-\sqrt{5}}}=\sqrt{\dfrac{\left(3-\sqrt{5}\right)^2}{9-5}}-\sqrt{\dfrac{\left(3+\sqrt{5}\right)^2}{9-5}}=\dfrac{3-\sqrt{5}}{2}-\dfrac{3+\sqrt{5}}{2}=-\sqrt{5}\)
\(F=\sqrt{3+\sqrt{5}}+\sqrt{7-3\sqrt{5}}-\sqrt{2}=\sqrt{\left(\sqrt{\dfrac{5}{2}}+\sqrt{\dfrac{1}{2}}\right)^2}+\sqrt{\left(\dfrac{3}{\sqrt{2}}-\sqrt{\dfrac{5}{2}}\right)^2}-\sqrt{2}=\sqrt{\dfrac{5}{2}}+\sqrt{\dfrac{1}{2}}+\dfrac{3}{\sqrt{2}}-\sqrt{\dfrac{5}{2}}-\sqrt{2}=2\sqrt{2}-\sqrt{2}=\sqrt{2}\)
26 tháng 8 2021
Bài 2:
Ta có: G-1
\(=\dfrac{\sqrt{x}-x+\sqrt{x}-1}{x-\sqrt{x}+1}\)
\(=\dfrac{-\left(x-2\sqrt{x}+1\right)}{x-\sqrt{x}+1}\)
\(=\dfrac{-\left(\sqrt{x}-1\right)^2}{x-\sqrt{x}+1}\le0\forall x\) thỏa mãn ĐKXĐ
hay \(G\le1\)
HP
29 tháng 8 2021
11.
\(\dfrac{5+\sqrt{5}}{5-\sqrt{5}}+\dfrac{5-\sqrt{5}}{5+\sqrt{5}}\)
\(=\dfrac{\left(5+\sqrt{5}\right)^2}{\left(5-\sqrt{5}\right)\left(5+\sqrt{5}\right)}+\dfrac{\left(5-\sqrt{5}\right)^2}{\left(5-\sqrt{5}\right)\left(5+\sqrt{5}\right)}\)
\(=\dfrac{25+5+10\sqrt{5}}{20}+\dfrac{25+5-10\sqrt{5}}{20}\)
\(=3\)
HP
29 tháng 8 2021
12.
\(\dfrac{3+2\sqrt{3}}{\sqrt{3}}+\dfrac{2+\sqrt{2}}{\sqrt{2}+1}-\dfrac{1}{2-\sqrt{3}}\)
\(=\dfrac{\sqrt{3}\left(\sqrt{3}+2\right)}{\sqrt{3}}+\dfrac{\sqrt{2}\left(\sqrt{2}+1\right)}{\sqrt{2}+1}-\dfrac{2+\sqrt{3}}{4-3}\)
\(=\sqrt{3}+2+\sqrt{2}-2-\sqrt{3}\)
\(=\sqrt{2}\)
24 tháng 8 2021
a: \(\dfrac{1}{3}\cdot\sqrt{18}-\sqrt{192}-\dfrac{\sqrt{33}}{\sqrt{11}}+3\cdot\sqrt{5\dfrac{1}{3}}\)
\(=\dfrac{1}{3}\cdot3\sqrt{2}-8\sqrt{3}-\sqrt{3}+3\cdot\dfrac{4}{\sqrt{3}}\)
\(=\sqrt{2}-7\sqrt{3}+4\sqrt{3}\)
\(=\sqrt{2}+3\sqrt{3}\)
b: Ta có: \(\sqrt{\left(2\sqrt{3}-5\right)^2}-2\cdot\sqrt{7+4\sqrt{3}}\)
\(=5-2\sqrt{3}-2\cdot\left(2+\sqrt{3}\right)\)
\(=5-2\sqrt{3}-4-2\sqrt{3}\)
\(=-4\sqrt{3}+1\)
10 tháng 7 2017
bạn nên tự nghiên cứu rồi giải đi chứ bạn đưa 1 loạt thế thì ai rảnh mà giải, với lại cứ bài gì không biết chưa chịu suy nghĩ đã hỏi rồi thì tiến bộ sao được, đúng không
30 tháng 9 2021
a: Ta có: \(A=\left(\dfrac{6+\sqrt{20}}{3+\sqrt{5}}+\dfrac{\sqrt{14}-\sqrt{2}}{\sqrt{7}-1}\right):\left(2+\sqrt{2}\right)\)
\(=\left(2+\sqrt{2}\right):\left(2+\sqrt{2}\right)\)
=1
b: Ta có: \(B=\sqrt{5-2\sqrt{6}}+\sqrt{5+2\sqrt{6}}-\dfrac{11}{2\sqrt{3}+1}\)
\(=\sqrt{3}-\sqrt{2}+\sqrt{3}+\sqrt{2}-2\sqrt{3}+1\)
=1
28 tháng 6 2021
Bạn chia nhỏ ra để nhận được câu tl sớm nhất nhé!Bạn đặt câu hỏi free mà để dày cộp như này khum ai dám làm =(((
28 tháng 6 2023
đề là rút gọn các biểu thức sau
nhờ mọi người giải giúp mình. cảm ơn mn nhìu
28 tháng 6 2023
a: \(=\dfrac{\sqrt{6-2\sqrt{5}}\left(3+\sqrt{5}\right)}{2\left(\sqrt{5}+1\right)}\)
\(=\dfrac{\left(\sqrt{5}-1\right)\left(3+\sqrt{5}\right)}{2\left(\sqrt{5}+1\right)}=\dfrac{3\sqrt{5}+5-3-\sqrt{5}}{2\sqrt{5}+2}\)
\(=\dfrac{2\sqrt{5}+2}{2\sqrt{5}+2}=1\)
b: \(=\dfrac{2\sqrt{5}\left(\sqrt{5}+\sqrt{2}\right)}{\sqrt{5}+\sqrt{2}}-2-2\sqrt{5}\)
=2căn 5-2-2căn 5
=-2
d: \(=\dfrac{\sqrt{2}}{2+\sqrt{3}+1}+\dfrac{\sqrt{2}}{2-\sqrt{3}+1}\)
\(=\dfrac{\sqrt{2}}{3+\sqrt{3}}+\dfrac{\sqrt{2}}{3-\sqrt{3}}\)
\(=\dfrac{3\sqrt{2}-\sqrt{6}+3\sqrt{2}+\sqrt{6}}{6}=\sqrt{2}\)
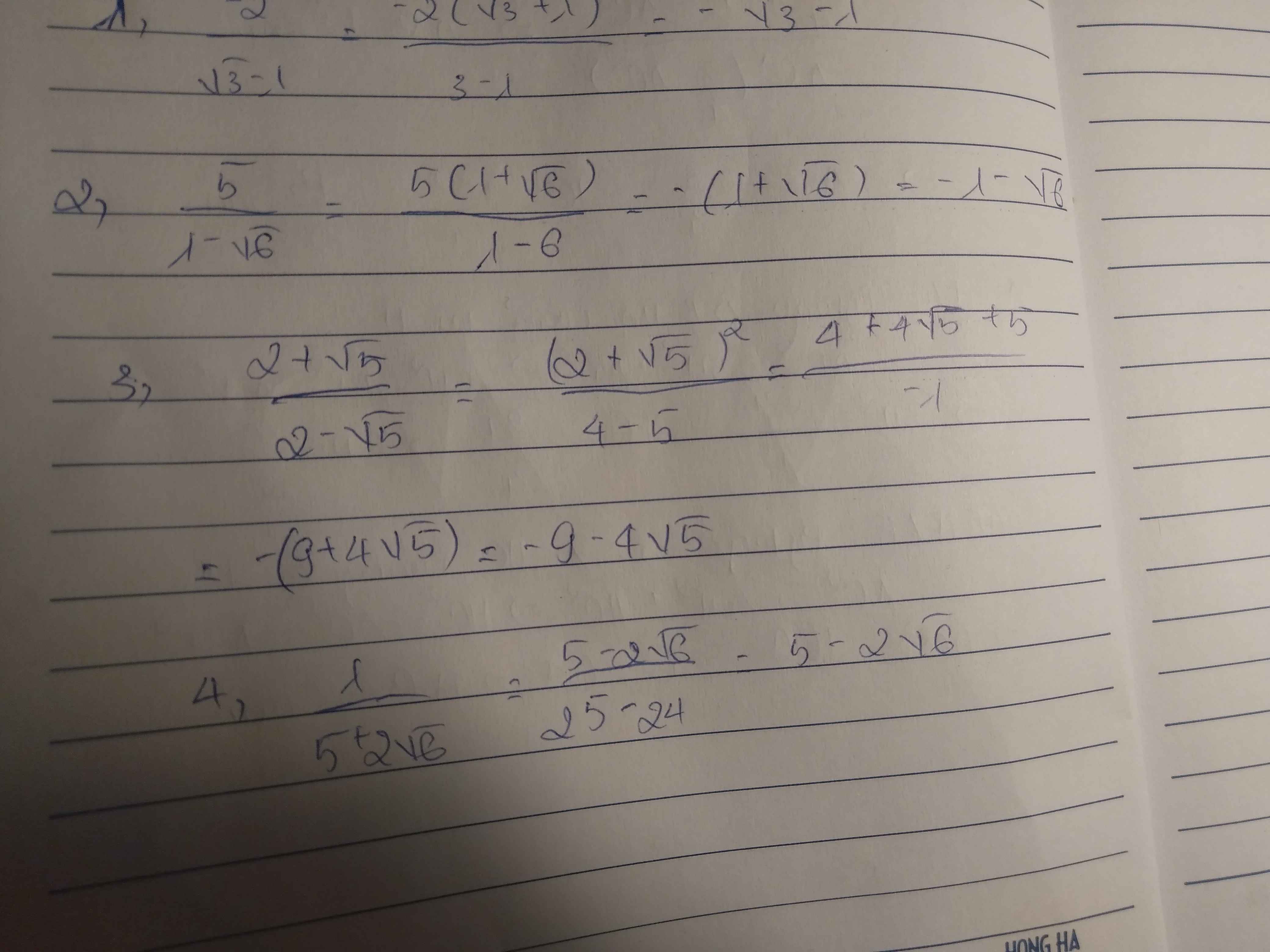
\(=\sqrt{\dfrac{\left(3\sqrt{5}-1\right)\left(2\sqrt{5}-3\right)}{\left(2\sqrt{5}+3\right)\left(2\sqrt{5}-3\right)}}-\sqrt{\dfrac{\left(11+\sqrt{5}\right)\left(7+2\sqrt{5}\right)}{\left(7+2\sqrt{5}\right)\left(7-2\sqrt{5}\right)}}\)
\(=\sqrt{\dfrac{33-11\sqrt{5}}{11}}-\sqrt{\dfrac{87+29\sqrt{3}}{29}}\)
\(=\sqrt{3-\sqrt{5}}-\sqrt{3+\sqrt{5}}=\dfrac{\sqrt{6-2\sqrt{5}}-\sqrt{6+2\sqrt{5}}}{\sqrt{2}}\)
\(=\dfrac{\sqrt{\left(\sqrt{5}-1\right)^2}-\sqrt{\left(\sqrt{5}+1\right)^2}}{\sqrt{2}}\)
\(=\dfrac{-2}{\sqrt{2}}=-\sqrt{2}\)