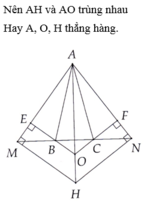
Cho ABC cân tại A. Lấy M, N thuộc BC sao cho BM = NC = MN
1) Chứng minh rằng : AM < AC. 2) Từ C kẻ Cx // AM cắt AN kéo dài tại D. Chứng minh rằng : BAM< MAN Mình đang gấp mong mọi người làm nhanh giúp mình
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
7 tháng 1 2022
a/
Ta có
\(\widehat{ABC}=\widehat{ACB}\) (2 góc ở đáy của tg cân ABC) (1)
\(\widehat{ABM}+\widehat{ABC}=\widehat{ACN}+\widehat{ACB}=180^o\)(2)
Từ (1) và (2) \(\Rightarrow\widehat{ABM}=\widehat{ACN}\)
Xét \(\Delta ABM\) và \(\Delta ACN\) có
AB=AC (cạnh bên của tg cân ABC)
BM=CN (gt)
\(\widehat{ABM}=\widehat{ACN}\left(cmt\right)\)
\(\Rightarrow\Delta ABM=\Delta ACN\left(c.g.c\right)\Rightarrow AM=AN\Rightarrow\Delta AMN\)cân tại A
b/
Xét tg vuông BME và tg vuông CNF có
\(\widehat{ABM}=\widehat{ACN}\left(cmt\right)\Rightarrow\widehat{AMN}=\widehat{ANM}\) (2 góc ở đáy của tg cân AMN)
BM=CN (gt)
\(\Rightarrow\Delta BME=\Delta CNF\) (Hai tg vuông có cạnh huyền và một góc nhọn tương ứng = nhau thì bằng nhau)
c/
Xét tg cân AMN có AM=AN (1)
\(\Delta BME=\Delta CNF\left(cmt\right)\Rightarrow ME=NF\) (2)
Từ (1) và (2) => AM-ME=AN-NF => AE=AF
Xét tg vuông AEO và tg vuông AFO có
AE=AF (cmt)
AO chung
\(\Rightarrow\Delta AEO=\Delta AFO\) (Hai tg vuông có cạnh huyền và cạnh góc vuông tương ứng bằng nhau thì bằng nhau)
\(\Rightarrow\widehat{OAE}=\widehat{OAF}\) => AO là phân giác của \(\widehat{MAN}\)
d/
Ta có
\(\widehat{HMN}=\widehat{HMA}-\widehat{AMN}=90^o-\widehat{AMN}\)
\(\widehat{HNM}=\widehat{HNA}-\widehat{ANM}=90^o-\widehat{ANM}\)
Mà \(\widehat{AMN}=\widehat{ANM}\)
\(\Rightarrow\widehat{HMN}=\widehat{HNM}\Rightarrow\Delta HMN\) cân tại H
Ta có
\(OE\perp AM;HM\perp AM\)=> OE//HM \(\Rightarrow\widehat{AOE}=\widehat{AHM}\) (góc đồng vị)
Chứng minh tương tự ta cũng có OF//HN \(\Rightarrow\widehat{AOF}=\widehat{AHN}\) (góc đồng vị)
Mà \(\Delta AEO=\Delta AFO\Rightarrow\widehat{AOE}=\widehat{AF}\)
\(\Rightarrow\widehat{AHM}=\widehat{AHN}\)=> HO là phân giác của \(\widehat{MHN}\)
Xét tg cân HMN có
HO là phân giác của \(\widehat{MHN}\)=> HO là đường trung trực của tg HMN (trong tg cân đường phân giác của góc ở đỉnh đồng thời là đường trung trực) => \(HO\perp MN\) tại trung điểm của MN
Xét tg cân AMN có
AO là đường phân giác của \(\widehat{MAN}\) (cmt) => AO là đường trung trực của tg AMN (trong tg cân đường phân giác của góc ở đỉnh đồng thời là đường trung trực) => \(AO\perp MN\) tại trung điểm của MN
=> AO trung HO (Từ 1 điểm trên đường thẳng chỉ duy nhất dựng được 1 đường thẳng vuông góc với đường thẳng đã cho)
=> A; O; H thẳng hàng
HH
20 tháng 2 2018
(Bạn tự vẽ hình giùm)
a/ \(\Delta AMB\)và \(\Delta ANC\)có: AB = AC (\(\Delta ABC\)cân tại A)
\(\widehat{B}=\widehat{C}\)(\(\Delta ABC\)cân tại A)
MB = NC (gt)
=> \(\Delta AMB\)= \(\Delta ANC\)(c - g - c) => AM = AN (hai cạnh tương ứng) (đpcm)
\(\Delta AHB\)và \(\Delta AHC\)có: AB = AC (\(\Delta ABC\)cân tại A)
BH = HC (H là trung điểm của BC)
Cạnh AH chung
=> \(\Delta AHB\)= \(\Delta AHC\)(c - c - c) => \(\widehat{AHB}=\widehat{AHC}\)(hai góc tương ứng)
Mà \(\widehat{AHB}+\widehat{AHC}\)= 180o (kề bù)
=> \(2\widehat{AHB}=180^o\)
=> \(\widehat{AHB}=90^o\)
=> \(AH\perp BC\)(đpcm)
b/ \(\Delta AHM\)vuông và \(\Delta AHN\)vuông có: AM = AN (cm câu a)
Cạnh AH chung
=> \(\Delta AHM\)vuông = \(\Delta AHN\)vuông (cạnh huyền - cạnh góc vuông) => HM = HN (hai cạnh tương ứng) => H là trung điểm MN
Ta có HB = HC = \(\frac{BC}{2}=\frac{6}{2}\)= 3 (cm)
và \(\Delta AHB\)vuông tại H => AH2 + HB2 = AB2 (định lý Pitago)
=> AH2 = AB2 - HB2
=> AH2 = 52 - 32
=> AH2 = 25 - 9
=> AH2 = 16
=> AH = \(\sqrt{16}\)(vì AH > 0)
=> AH = 4 (cm)
Ta lại có BM = MN = NC (gt)
Mà BM + MN + NC = BC
=> 3BM = 6
=> BM = MN = NC = 2
=> HM = HN = 1
và \(\Delta AHM\)vuông tại H => AM2 = AH2 + MH2 (định lý Pitago)
=> AM2 = 42 + 12
=> AM2 = 16 + 1
=> AM2 = 17
=> AM = \(\sqrt{17}\)(cm) (vì AM > 0)
19 tháng 1 2023
a: Xét ΔBAM và ΔCAP có
BM=CP
BA=CA
AM=AP
=>ΔBAM=ΔCAP
=>góc BAM=góc CAP
=>góc BAM+góc MAN=góc CAP+góc MAN
=>góc MAN<góc NAP
b: Xét ΔMAN và ΔQAN co
AM=AQ
góc MAN=góc QAN
AN chung
=>ΔMAN=ΔQAN
=>NM=NQ
mà NP>NM
nên NP>NQ