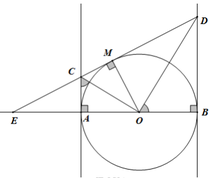
Cho (O) đường kính AB . Trên tia đối của tia AB lấy điểm E . Từ E ,A,B kẻ tiếp tuyến với nửa đường tròn . Tiếp tuyến kẻ từ E cắt 2 tiếp tuyến A và B lần lượt tại C và D
a, Gọi M là tiếp điểm của tiếp tuyến kẻ từ E đến nửa đường tròn . CM : ACMO nội tiếp
b, DM.CE = CM.DE
c, gọi N là giao điểm của AD và BD . CM : MN//BD



a/
Ta có M và A cùng nhìn OC dưới 1 góc \(90^o\) => ACMO là tứ giác nội tiếp
b/
Xét tg vuông BED và tg vuông AEC có \(\widehat{BED}\) chung
=> tg BED đồng dạng với tg AEC (g.g.g)
\(\Rightarrow\dfrac{DB}{CA}=\dfrac{DE}{CE}\)
Mà
\(DB=DM;CA=CM\) (Hai tiếp tuyến cùng xp từ 1 điểm...)\(\Rightarrow\dfrac{DB}{CA}=\dfrac{DM}{CM}=\dfrac{DE}{CE}\Rightarrow DM.CE=CM.DE\)
c/
Ta có
\(CA\perp AB\left(gt\right);DB\perp AB\left(gt\right)\) => CA//DB
\(\Rightarrow\dfrac{BN}{CN}=\dfrac{DB}{CA}\) (Talet)
Mà \(\dfrac{DM}{CM}=\dfrac{DB}{CA}\left(cmt\right)\)
\(\Rightarrow\dfrac{BN}{CN}=\dfrac{DM}{CM}\) => MN//BD (Talet đảo trong tam giác)