Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
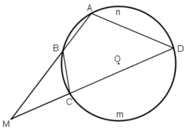
Gọi B', C' lần lượt là giao điểm khác A của AB, AC với (O').
Do BM, CM là tiếp tuyến của (O') nên ta dễ dàng chứng minh được:
\(BM^2=BA.BB'\); \(CM^2=CA.CC'\)
\(\Rightarrow\dfrac{BM^2}{CM^2}=\dfrac{BA.BB'}{CA.CC'}\). (1)
\(\Delta AOC\sim\Delta AO'C'(g.g)\Rightarrow \frac{AC}{AC'}=\frac{AO}{AO'}\).
Tương tự, \(\frac{AB}{AB'}=\frac{AO}{AO'}\).
Do đó \(\dfrac{AB}{AB'}=\dfrac{AC}{AC'}\Rightarrow\dfrac{AB}{BB'}=\dfrac{AC}{CC'}\Rightarrow\dfrac{AB}{AC}=\dfrac{BB'}{CC'}\). (2)
Từ (1), (2) suy ra \(\dfrac{BM}{CM}=\dfrac{AB}{AC}\).
Theo tính chất đường phân giác đảo thì AM là đường phân giác ngoài của tam giác ABC
\(\Rightarrow\widehat{MAB}+\widehat{MAC}=180^o\Rightarrow180^o+\widehat{BAC}=2\widehat{EAC}\)
\(\Rightarrow180^o-\widehat{EAC}=\dfrac{180^o-\widehat{BAC}}{2}\). (3)
Các tứ giác FDEA, DBAC nội tiếp nên \(\widehat{FDB}=180^o-\widehat{EAC};\widehat{BDC}=180^o-\widehat{BAC}\). (4)
Từ (3), (4) suy ra \(\widehat{FDB}=\dfrac{\widehat{BDC}}{2}\) nên DF là phân giác góc BDC.
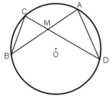
TH1: M nằm trong đường tròn.
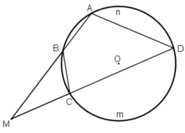
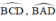là hai góc nội tiếp cùng chắn cung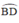 
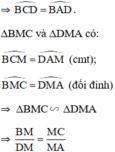
⇒ MA.MB = MC.MD
TH2: M nằm ngoài đường tròn.
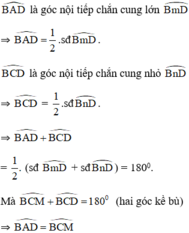
ΔMBC và ΔMDA có:
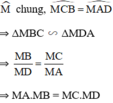
Kiến thức áp dụng
+ Góc nội tiếp chắn một cung có số đo bằng một nửa số đo của cung đó.
+ Hai góc nội tiếp chắn cùng một cung thì có số đo bằng nhau.
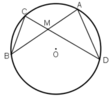
TH1: M nằm trong đường tròn.
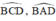là hai góc nội tiếp cùng chắn cung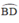 
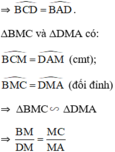
⇒ MA.MB = MC.MD
TH2: M nằm ngoài đường tròn.
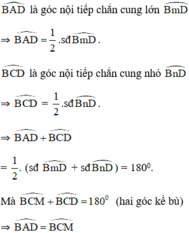
ΔMBC và ΔMDA có:
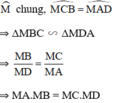
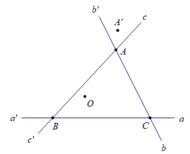
a. Giả sử ba đường thẳng aa’, bb’ và cc’ cắt nhau từng đôi một tại ba điểm A, B, C (hình vẽ). Điểm O cần vẽ là giao điểm của hai tia AO và BO sao cho tia AO nằm giữa hai tia AB và AC, tia BO nằm giữa hai tia BA và BC.
b. Điểm A’ nằm trên tia AA’ sao cho tia AA’ nằm giữa hai tia Ab’ và Ac, A’ và O cùng nằm trong một nửa mặt phẳng có bờ là đường thẳng BC.
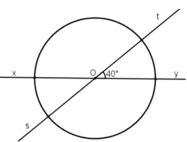
Ta có :
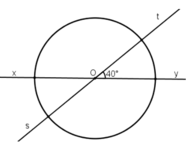
\(\widehat{xOs}\)= 400(theo giải thiết)
\(\widehat{tOy}\)=400( đối đỉnh với \(\widehat{xOs}\))
\(\widehat{xOt}\) + \(\widehat{tOy}\)= 1800
\(\Rightarrow\widehat{xOt}\) = \(\widehat{tOy}\) \(=180^0-40^0=140^0\)
\(\widehat{yOs}=140^0\)(đối đỉnh với \(\widehat{xOt}\))
\(\widehat{xOy}=\widehat{sOt}=180^0\)
a: góc ONM+góc OPM=180 độ
=>ONMP nội tiếp
b: góc OHM=góc ONM=90 độ
=>OHNM nội tiếp
=>góc MON=góc MHN
Tam giác AO’C nội tiếp trong đường tròn (O) có O’C là đường kính nên 
Suy ra: CA ⊥ O’A tại điểm A
Vậy CA là tiếp tuyến của đường tròn (O’)
Tam giác BO’C nội tiếp trong đường tròn (O) có O’C là đường kính nên 
Suy ra: CB ⊥ O’B tại điểm B
Vậy CB là tiếp tuyến của đường tròn (O’)
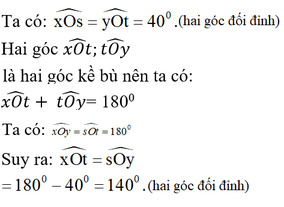
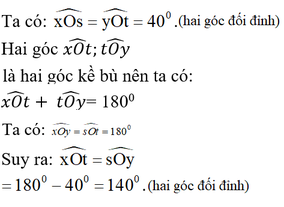
Gọi giao điểm của MB với (O;r) là H, giao điểm của MD với (O;r) là K
Theo đề, ta có: OH\(\perp\)MB tại H và OK\(\perp\)MD tại K
Xét (O) có
OH,OK là khoảng cách từ tâm O đến cách dây AB,CD
AB,CD là các dây
OH=OK(=r)
Do đó: AB=CD
ΔOAB cân tại O
mà OH là đường cao
nên H là trung điểm của AB
=>HA=HB=AB/2
Ta có: ΔOCD cân tại O
mà OK là đường cao
nên K là trung điểm của CD
=>\(CK=KD=\dfrac{CD}{2}\)
mà CD=AB và \(HA=HB=\dfrac{AB}{2}\)
nên CK=KD=HA=HB
Xét ΔOHM vuông tại H và ΔOKM vuông tại K có
OH=OK
OM chung
Do đó: ΔOHM=ΔOKM
=>MH=MK
Ta có: MA+AH=MH
MC+CK=MK
mà AH=CK và MH=MK
nên MA=MC
Xét ΔMBD có \(\dfrac{MA}{AB}=\dfrac{MC}{CD}\)
nên AC//BD
=>\(sđ\stackrel\frown{AB}=sđ\stackrel\frown{CD}\)