ông Nam có 500 tr đông. Một phân ô mua trái phiêu với lãi suất là 8%, phần còn lại ô gửi tiết kiệm lãi suất 5% cho một năm. Cuối năm ô thu được tiền lãi là 35,5tr tính số tiền đầu tư ban đầu ?( chú ý chỉ có tiền lãi thôi) |
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


SỐ tiền gửi tiết kiệm là:
\(160.2\cdot10^6\cdot\dfrac{100\%}{106.8\%}=150000000\left(đồng\right)\)

Giải:
Gọi số tiền ông Sáu gửi ban đầu là x.
Theo đề bài ta có:
Số tiền lãi sau 1 năm ông Sáu nhận được là : 0,06x (đồng)
Số tiền lãi có được 1 năm của ông Sáu là : x + 0,06x = 1,06x (đồng)
Số tiền lãi năm thứ 2 ông Sáu nhận được là : 1,06x. 0,06 = 0,0636x (đồng)
Do vậy, số tiền tổng cộng sau 2 năm ông Sáu nhận được là : 1,06x + 0,0636x = 1,1236x (đồng)
Mặt khác: 1,1236x = 112360000 nên x = 100000000(đồng) hay 100 triệu đồng
Vậy ban đầu ông Sáu đã gửi 100 triệu đồng.
Tổng % lãi suất trong 2 năm là :
6% . 2 = 12%
Số tiền lãi trong 2 năm là :
112360000 . 12% = 13483200
=> Tiền ông Sáu gửi là :
112360000 - 13483200 = 98876800

Số tiền cả gốc lẫn lãi sau 1 năm là:
\(100000000\cdot\left(1+5\%\right)=105000000\left(đ\right)\)
Số tiền cả gốc lẫn lãi sau 2 năm tiếp là:
\(105000000\cdot\left(1+5\%\right)=110250000\left(đ\right)\)
Số tiền cả gốc lẫn lãi sau 3 năm tiếp là:
\(110250000\cdot\left(1+5\%\right)=115762500\left(đ\right)\)
Vậy: Cứ như thế sau ba năm thì số tiền cả gốc lẫn lãi là \(115762500\) đồng
(\(100\%=\dfrac{100}{100}=1\)).

Đáp án B
Gọi A là số tiền gốc ban đầu, lãi suất r/năm, số tiền gửi thêm là a (triệu đồng)
Sau năm đầu tiên, số tiền cả gốc lẫn lãi mà ông Minh nhận đc là A(1+r)
Sau năm thứ 2, cả gốc và lãi ông nhận được là
![]()
Sau năm thứ 3, cả gốc và lãi ông nhận được:
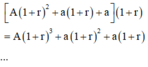
Sau năm thứ n, ông Minh nhận được số tiền:
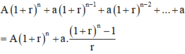
Thay số: sau 10 năm ông Minh nhận về cả gốc lẫn lãi là
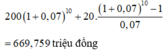
Đáp án B
Gọi A là số tiền gốc ban đầu, lãi suất r/năm, số tiền gửi thêm là a (triệu đồng)
Sau năm đầu tiên, số tiền cả gốc lẫn lãi mà ông Minh nhận đc là A(1+r)
Sau năm thứ 2, cả gốc và lãi ông nhận được là
![]()
Sau năm thứ 3, cả gốc và lãi ông nhận được:
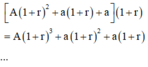
Sau năm thứ n, ông Minh nhận được số tiền:
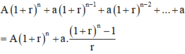
Thay số: sau 10 năm ông Minh nhận về cả gốc lẫn lãi là
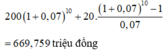

Đáp án C
Gọi A là số tiền gốc ban đầu, lãi suất r / năm, số tiền gửi thêm là a (triệu đồng).
Sau năm đầu tiên, số tiền cả gốc lẫn lãi mà ông Minh nhận được là: A 1 + r
Sau năm thứ 2, cả gốc và lãi ông nhận được là: A 1 + r + a 1 + r = A 1 + r 2 + a 1 + r
Sau năm thứ 3, cả gốc và lãi ông nhận được:
A 1 + r 2 + a 1 + r + a 1 + r = A 1 + r 3 + a 1 + r 2 + a 1 + r
…
Sau năm thứ n, ông Minh nhận được số tiền:
A 1 + r n + a 1 + r n − 1 + a 1 + r n − 2 + . .. + a = A 1 + r n + a . 1 + r n − 1 r
Thay số: sau 10 năm ông Minh nhận về cả gốc lẫn lãi là
200 1 + 0 , 07 10 + 20. 1 + 0 , 07 10 − 1 0 , 07 = 669 , 759 triệu đồng.

Đáp án D
Số tiền mà ông An nhận được là
T = 50.10 6 . 1 + 8 , 4 4 % 3 . 1 + 12 4 % 4 ≈ 59.895.767 đ ồ n g .
Đáp án D
Số tiền mà ông An nhận được là
T = 50.10 6 . 1 + 8 , 4 4 % 3 . 1 + 12 4 % 4 ≈ 59.895.767 đồng .

Số tiền lãi của người đó có là :
\(16080000-15000000=1080000\left(đồng\right)\)
Tỉ số phần trăm của tiền lãi và số tiền đã gửi lúc đầu đó là :
\(1080000:15000000.100=7,2\%\)
Số tiền lãi người đó có được sau 1 năm là:
16 080 000 - 15 000 000 = 1 080 000 (đồng)
Lãi suất tiết kiệm trong 1 năm là:
1 080 000 : 15 000 000 = 0,072
0,072 = 7,2%
đáp số
Gọi số tiền mua trái phiếu là x (triệu đồng) và số tiền gửi tiết kiệm là y (triệu đồng) với x;y>0
Do tổng cộng ông có 500tr nên ta có pt: \(x+y=500\) (1)
Số tiền lãi từ trái phiếu sau 1 năm là: \(x.8\%=\dfrac{2x}{25}\) (triệu đồng)
Số tiền lãi từ tiết kiệm sau 1 năm là: \(y.5\%=\dfrac{y}{20}\) (triệu đồng)
Do sau 1 năm ông thi được 35,5tr tiền lãi nên ta có:
\(\dfrac{2x}{25}+\dfrac{y}{20}=35,5\) (2)
Từ(1) và (2) ta có hệ:
\(\left\{{}\begin{matrix}x+y=500\\\dfrac{2x}{25}+\dfrac{y}{20}=35,5\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=350\\y=150\end{matrix}\right.\)
Vậy ông đầu tư 350tr vào trái phiếu và 150tr để gửi tiết kiệm
*Đã có người trả lời*=>Bấm để xem đáp án