Mn ơi giúp em bài 3 với ạ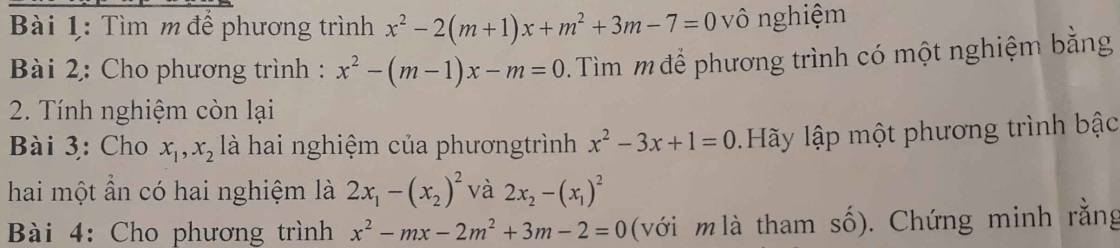
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 4:
a: \(A=\left(x-5\right)\left(2x+3\right)-2x\left(x-3\right)+x+7\)
\(=2x^2+3x-10x-15-2x^2+6x+x+7\)
=-8

Bài 5:
a: \(x\left(x-1\right)-x^2+4x=-3\)
\(\Leftrightarrow x^2-x-x^2+4x=-3\)
hay x=-1
i: \(x^2-9x+8=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-8\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=8\end{matrix}\right.\)

a) - Dùng quỳ tím:
+ Hóa đỏ -> dd H2SO4
+ Hóa xanh -> dd NaOH
+ Không đổi màu -> dd NaCl
b) - Dùng quỳ tím:
+ Hóa xanh -> dd Ca(OH)2
+ Hóa đỏ -> dd H2SO4, dd HCl
- Dùng dd BaCl2:
+ Có kết tủa trắng BaSO4 -> dd H2SO4
+ Không có kt trắng -> dd HCl
PTHH: H2SO4 + BaCl2 -> BaSO4 (kt trắng) + 2 HCl

1.
\(\Delta'=\left(m+1\right)^2-\left(m^2+3m-7\right)=-m+8\)
Phương trình đã cho vô nghiệm khi và chỉ khi \(\Delta'< 0\)
\(\Rightarrow-m+8< 0\)
\(\Rightarrow m>8\)

2.
Do pt có 1 nghiệm bằng 2, thay \(x=2\) vào pt ta được:
\(2^2-2\left(m-1\right)-m=0\)
\(\Rightarrow6-3m=0\Rightarrow m=2\)
Khi đó nghiệm còn lại (tính theo định lý Viet là):
\(x_1x_2=-m\Rightarrow x_2=\dfrac{-m}{x_1}=\dfrac{-2}{2}=-1\)
x^2-(m-1)x-m=0 (*)
Ta có x=2 thế vào pt(*),ta có:
2^2-(m-1).2-m=0
<=> 4-2m+2-m=0
<=> -3m=-6
<=> m=2
Thế m=2 vào lại pt(*),ta lại có:
x^2-(2-1)x-2=0
<=> x^2-x-2=0
<=> x^2-2x+x-2=0
<=> (x^2-2x)+(x-2)=0
<=>x(x-2)+(x-2)=0
<=> (x-2)(x+1)=0
<=> x-2=0 hoặc x+1=0
<=>x=2 hoặc x=-1
Vậy S={−1;2}

refer
1/ I like table tennis and that’s why I spend a lot of time on that game.
=>I spend a lot of time on table tennis because I like it.
2/ Because the weather was cold, we had to cancel our picnic.
=> The weather was cold, so we had to cancel our picnic.
3/ I won’t forget to phone her. You know, I like her so much.
=> You know I like her so much so I won't forget to phone her
4/ They tried their best to complete the course and that was why they passed.
=> they tried their best to complete the course, so they passed
5/ I love my city so much, so I think I will stay and work here in my city.
=> I think I will stay and word in my city because I love it so much.
1 Because I like table tennis, I spend a lot of time on that game
2 The weather was so cold that we had to cancel our picnic
3 I won't forget to phone her because I like her so mich
4 They pass the course because they tried their best to complete the course
5 Because I love my city so much, I think I will stay and work here in my city




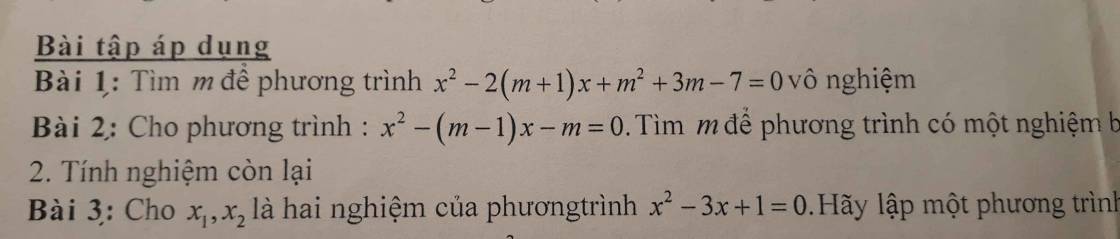
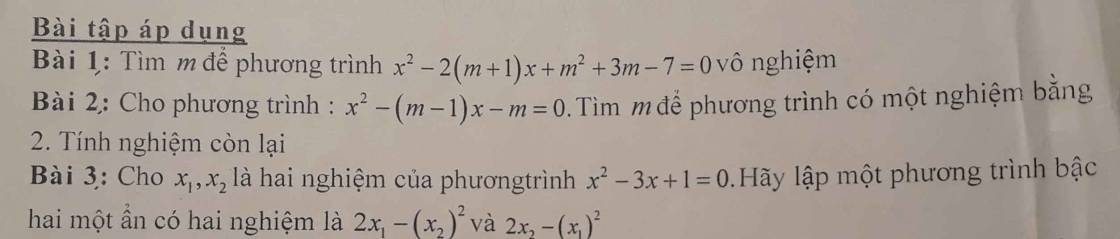






Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=3\\x_1x_2=1\end{matrix}\right.\)
Gọi \(x_3;x_4\) là các nghiệm của pt cần tìm, ta có:
\(\left\{{}\begin{matrix}x_3+x_4=2x_1-x_2^2+2x_2-x_1^2\\x_3x_4=\left(2x_1-x_2^2\right)\left(2x_2-x_1^2\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x_3+x_4=2\left(x_1+x_2\right)-\left(x_1+x_2\right)^2+2x_1x_2\\x_3x_4=4x_1x_2-2x_1^3-2x_2^3+\left(x_1x_2\right)^2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x_3+x_4=2\left(x_1+x_2\right)-\left(x_1+x_2\right)^2+2x_1x_2\\x_3x_4=4x_1x_2-2\left[\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)\right]+\left(x_1x_2\right)^2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x_3+x_4=2.3-3^2+2.1=-1\\x_3x_4=4.1-2\left(3^3-3.1.3\right)+1^2=-31\end{matrix}\right.\)
Theo định lý Viet đảo, pt cần tìm có dạng:
\(x^2+x-31=0\)