Vẽ hệ trục tọa độ Oxy và xác định các điểm A(0; 4) B(-3;0) C(3;0) a.Tính chu vi và diện tích của tam giác ABC b. Tính khoảng cách từ C đến AB.
Xin được mọi người giúp ạ.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Trên hình vẽ 0, A, B, C, D là vị trí của các điểm biểu diễn các cặp giá trị tương ứng của x và y trong câu a.
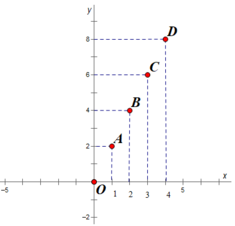

Trên trục tọa độ thì bạn lấy điểm A nằm trên trục Ox có hoành độ bằng 3, còn điểm B thì bạn lấy trên trục Oy có tung độ là 1 nha

a: Tọa độ A là:
y=0 và -2x+2=0
=>x=1 và y=0
=>A(1;0)
Tọa độ B là:
x=0 và y=-2x+2
=>x=0 và y=-2*0+2=2
=>B(0;2)
b: C thuộc Ox nên C(x;0)
D thuộc Oy nên D(0;y)
ABCD là hình thoi nên AB=AD và vecto AB=vecto DC
A(1;0); B(0;2); C(x;0); D(0;y)
\(\overrightarrow{AB}=\left(-1;2\right);\overrightarrow{DC}=\left(x;-y\right)\)
\(AB=\sqrt{\left(0-1\right)^2+\left(2-0\right)^2}=\sqrt{5}\)
\(AD=\sqrt{\left(0-1\right)^2+\left(y-0\right)^2}=\sqrt{y^2+1}\)
vecto AB=vecto DC
=>x=-1 và -y=2
=>x=-1 và y=-2
AB=AD
=>y^2+1=5
=>y^2=4
=>y=2(loại) hoặc y=-2(nhận)
Vậy: x=-1 và y=-2
=>C(-1;0); D(0;-2)
Gọi phương trình (d2) có dạng là y=ax+b
(d2) đi qua C và D nên ta có hệ phương trình:
a*(-1)+b=0 và 0*a+b=-2
=>b=-2 và -a=-b=2
=>a=-2 và b=-2
=>y=-2x-2
c: (d1): y=-2x+2 và (d2): y=-2x-2
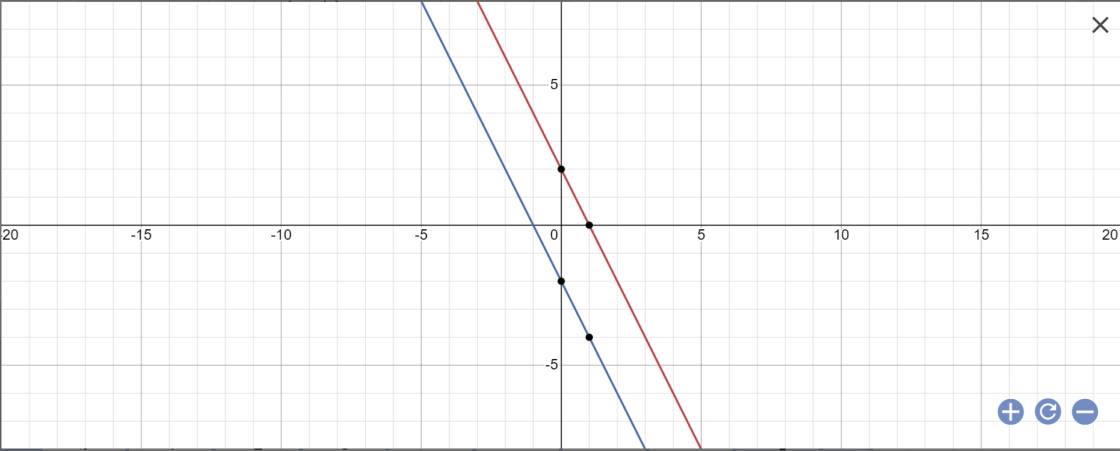
a: A(0;4); B(-3;0); C(3;0)
\(AB=\sqrt{\left(-3-0\right)^2+\left(0-4\right)^2}=5\)
\(AC=\sqrt{\left(3-0\right)^2+\left(0-4\right)^2}=5\)
\(BC=\sqrt{\left(3+3\right)^2+\left(0-0\right)^2}=6\)
Chu vi tam giác ABC là:
5+5+6=16
Xét ΔABC có \(cosBAC=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}=\dfrac{5^2+5^2-6^2}{2\cdot5\cdot5}=\dfrac{7}{25}\)
=>\(sinBAC=\sqrt{1-\left(\dfrac{7}{25}\right)^2}=\dfrac{24}{25}\)
Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC\cdot sinBAC\)
\(\dfrac{1}{2}\cdot5\cdot5\cdot\dfrac{24}{25}=\dfrac{24}{2}=12\)
b: Khoảng cách từ C đến AB là:
\(2\cdot\dfrac{S_{ABC}}{AB}=\dfrac{2\cdot12}{5}=\dfrac{24}{5}=4,8\)
Xin cảm ơn ạ.