cho ΔABC = ΔPQR. biết A= 50 độ và B-C = 50 độ.
a, chứng minh rằng ΔPQR là tam giác vuông
b, chỉ ra các cặp cạnh bằng nhau của mỗi tam giác
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải:
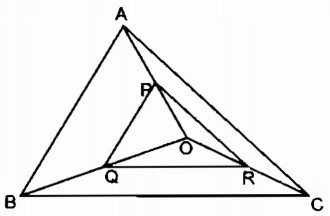
a. Trong tam giác AOB, ta có:
P trung điểm của OA (gt)
Q trung điểm của OB (gt)
Suy ra: PQ là đường trung bình của ∆ OAB.
Suy ra: PQ=12ABPQ=12AB
(tính chất đường trung bình của tam giác )
Suy ra: PQAB=12PQAB=12 (1)
Trong tam giác OAC, ta có:
P trung điểm của OA (gt)
R trung điểm của OC (gt)
Suy ra: PR là đường trung bình của tam giác OAC.
Suy ra: PR=12ACPR=12AC (tính chất đường trung bình của tam giác )
Suy ra: PRAC=12PRAC=12 (2)
Trong tam giác OBC, ta có:
Q trung điểm của OB (gt)
R trung điểm của OC (gt)
Suy ra: QR là đường trung bình của tam giác OBC.
Suy ra: QR=12BCQR=12BC (tính chất đường trung bình của tam giác )
Suy ra: QRBC=12QRBC=12 (3)
Từ (1), (2) và (3) suy ra: PQAB=PRAC=QRBC=12PQAB=PRAC=QRBC=12
Vậy ∆ PQR đồng dạng ∆ ABC (c.c.c)
b. Gọi p’ là chu vi tam giác PQR.
Ta có: PQAB=PRAC=QRBC=PQ+PR+QRAB+AC+BC=p′pPQAB=PRAC=QRBC=PQ+PR+QRAB+AC+BC=p′p
Vậy: p′p=12⇒p′=12p=12.543=271,5p′p=12⇒p′=12p=12.543=271,5 (cm)

a. Xét △OAB có:
Q là trung điểm OB, P là trung điểm OA (gt).
\(\Rightarrow\) PQ là đường trung bình của △OAB.
\(\Rightarrow PQ=\dfrac{1}{2}AB\)
\(\Rightarrow\dfrac{PQ}{AB}=\dfrac{\dfrac{1}{2}AB}{AB}=\dfrac{1}{2}\)
-Tương tự: \(\dfrac{QR}{BC}=\dfrac{1}{2};\dfrac{PR}{AC}=\dfrac{1}{2}\)
-Xét △PQR và △ABC có:
\(\dfrac{PQ}{AB}=\dfrac{QR}{BC}=\dfrac{PR}{AC}\left(=\dfrac{1}{2}\right)\)
\(\Rightarrow\)△PQR ∼ △ABC (c-c-c).
b. Ta có: △PQR ∼ △ABC (cmt).
\(\Rightarrow\dfrac{S_{PQR}}{S_{ABC}}=\left(\dfrac{PQ}{AB}\right)^2=\left(\dfrac{1}{2}\right)^2=\dfrac{1}{4}\)
\(\Rightarrow S_{PQR}=\dfrac{1}{2}S_{ABC}=\dfrac{1}{2}.540=270\left(cm^2\right)\)

Bài 1:
a)
Góc ở đáy = (180o-50o) : 2 = 65o
b)
Góc ở đỉnh = 180o - (50o x 2) = 80o

a: góc ABC=180-50-70=60 độ
b: Vì góc IBC=1/2*góc ABC
nên BI là phân giác của góc ABC
Vì góc ICB=1/2*góc ACB
nên CI là phân giác của góc ACB
c: Xét ΔBFI vuông tại F và ΔBDI vuông tại D có
BI chung
góc FBI=góc DBI
=>ΔBFI=ΔBDI
=>ID=IF
Xét ΔCDI vuông tại D và ΔCEI vuông tại E co
CI chung
góc DCI=góc ECI
=>ΔCDI=ΔCEI
=>ID=IE=IF
=>I là giao của 3 đường trung trực ΔDEF

Ta có : \(\widehat{A}=80^o;\widehat{B}=50^o\Rightarrow\widehat{C}=180^o-\widehat{A}-\widehat{B}=180^o-80^o-50^o=50^o\)
\(\Rightarrow\widehat{C}=\widehat{B}< \widehat{A}\)
\(a,\) Cạnh lớn nhất là cạnh BC, bé nhất là cạnh AC
\(b,\) Tam giác ABC là tam giác cân vì có \(\widehat{C}=\widehat{B}=45^o\)

GK=9cm
nên AC=9cm
BC=13,5cm
MN=7cm
nên AB=7cm
\(C_{ABC}=C_{MNP}=C_{GHK}=29,5\left(cm\right)\)

a,
\(\Delta ABC=\Delta PQR\\ \Rightarrow\widehat{A}=\widehat{P}=50^o\\ \widehat{B}=\widehat{Q}\)
Xét \(ABC\) có
\(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
\(\Rightarrow\widehat{B}+\widehat{C}=130^o\\ \Rightarrow\widehat{B}=130^o-\widehat{C}\)
\(\widehat{B}-\widehat{C}=50^o\\ \Rightarrow130^o-2\widehat{C}=50^o\\ \Rightarrow\widehat{C}-40^o\\ \Rightarrow\widehat{B}=90^o=\widehat{Q}\)
\(\Rightarrow PQR\) là tam giác vuông
b, \(\Delta ABC=\Delta PQR\\ \Rightarrow\left\{{}\begin{matrix}AC=PR\\AB=PQ\\BC=QR\end{matrix}\right.\)