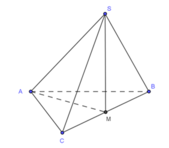
cho hình chóp S.ABC, SA vuông góc (ABC) đáy là tam giác ABC vuông cân tại B, AB = a và SA \(=a\sqrt{2}\)
a) tính góc giữa đường thẳng SA và AB
b) tính góc giữa đường thẳng SB và BA
c) I là trung điểm AC. Tính góc giữa đường thẳng SI và BI
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(\widehat{SB;AB}=\widehat{SBA}\)
SA\(\perp\)(ABC)
=>\(SA\perp AB;SA\perp AC;SA\perp BC\)
Xét ΔSAB vuông tại A có \(tanSBA=\dfrac{SA}{AB}=\dfrac{a\sqrt{3}}{a}=\sqrt{3}\)
=>\(\widehat{SBA}=60^0\)
=>\(\widehat{SB;AB}=60^0\)
b:
\(\widehat{SC;AC}=\widehat{SCA}\)
Xét ΔSAC vuông tại A có \(tanSCA=\dfrac{SA}{AC}=\dfrac{a\sqrt{3}}{a}=\sqrt{3}\)
nên \(\widehat{SCA}=60^0\)
=>\(\widehat{SC;AC}=60^0\)
c: ΔABC đều có AM là đường trung tuyến
nên \(AM=BC\cdot\dfrac{\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{2}\)
Ta có: SA\(\perp\)(ABC)
AM\(\subset\)(ABC)
Do đó: SA\(\perp\)AM
=>ΔSAM vuông tại A
\(\widehat{SM;AM}=\widehat{SMA}\)
Xét ΔSMA vuông tại A có \(tanSMA=\dfrac{SA}{AM}=\dfrac{a\sqrt{3}}{\dfrac{a\sqrt{3}}{2}}=2\)
=>\(\widehat{SMA}\simeq63^026'\)
=>\(\widehat{SM;AM}\simeq63^026'\)
a.
Góc giữa SB và AB là góc \(\widehat{SBA}\)
Trong tam giác vuông SAB:
\(tan\widehat{SBA}=\dfrac{SA}{AB}=\dfrac{a\sqrt{3}}{a}=\sqrt{3}\)
\(\Rightarrow\widehat{SBA}=60^0\)
b.
Góc giữa SC và AC là góc \(\widehat{SCA}\)
\(tan\widehat{SCA}=\dfrac{SA}{AC}=\sqrt{3}\Rightarrow\widehat{SCA}=60^0\)
c.
Góc giữa SM và AM là góc \(\widehat{SMA}\)
AM là trung tuyến tam giác đều \(\Rightarrow AM=\dfrac{a\sqrt{3}}{2}\)
\(\Rightarrow tan\widehat{SMA}=\dfrac{AM}{SA}=2\Rightarrow\widehat{SMA}=60^026'\)

Đáp án B
Gọi I là hình chiếu của điểm S trên mặt phẳng (ABC). Do S A = S B = S C nên I A = I B = I C ⇒ I là tâm đường tròn ngoại tiếp Δ A B C . Mà Δ A B C vuông cân tại A nên I là trung điểm của BC và I A = I B = I C = 1 2 B C = a 2 2 .
Ta có IA là hình chiếu của SA trên mặt phẳng (ABC) nên S A , A B C ^ = S A , I A ^ = S A I ^ = 45 0 .
Do Δ S I A vuông tại I nên Δ S A I vuông cân tại I, khi đó : S I = I A = a 2 2 ⇒ d S ; A B C = S I = a 2 2

Đáp án B
Hình chiếu của S xuống đáy ABC là tâm của đáy tức là M với M là trung điểm của BC.
Ta có ![]()
Vì ABC là tam giác vuông cân nên H cũng là trung điểm của vì thế
![]()
Ta có: ![]()
![]() =
a
2
2
=
a
2
2

Đáp án B
Gọi I là hình chiếu của điểm S trên mặt phẳng (ABC). Do SA = SB = SC nên IA = IB = IC => I là tâm đường tròn ngoại tiếp ∆ ABC . Mà ∆ ABC vuông cân tại A nên I là trung điểm của BC và IA = IB = IC = BC/2 = a 2 2
Ta có IA là hình chiếu của SA trên mặt phẳng (ABC) nên
![]()
Do ∆ SIA vuông tại I nên vuông cân tại I, khi đó :
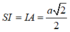
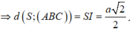

Đáp án B
Hình chiếu của S xuống đáy ABC là tâm của đáy tức là M với M là trung điểm của .
Ta có S A , A B C ^ = S A , A M ^ = S A M = 45 0
Vì ABC là tam giác vuông cân nên H cũng là trung điểm của BC vì thế
A M = 1 2 B C = a 2 2
ta có
d S ; A B C = S M = A M . tan S A M = a 2 2 . tan 45 0 = a 2 2

a: BC vuông góc AM
BC vuông góc SA
=>BC vuông góc (SAM)
b: BC vuông góc (SAM)
=>BC vuông góc SM
=>(SM;(ABC))=90 độ

Xét tam giác ABC có : \(BC=AB.\tan60^0=2a\sqrt{3}\Rightarrow S_{\Delta ABC}=2a^2\sqrt{3}\)
\(V_{S.ABCD}=\frac{1}{3}SA.S_{\Delta ABC}=\frac{1}{3}a\sqrt{3}.2a^2\sqrt{3}=2a^3\)
- Gọi N là trung điểm cạnh SA. Do SB//(CMN) nên d(SB. CM)=d(SB,(CMN))
=d(B,(CMN))
=d(A,(CMN))
- Kẻ \(AE\perp MC,E\in MC\) và kẻ \(AH\perp NE,H\in NE\), ta chứng minh được \(AH\perp\left(CMN\right)\Rightarrow d\left(A,\left(CMN\right)\right)=AH\)
Tính \(AE=\frac{2S_{\Delta AMC}}{MC}\) trong đó :
\(S_{\Delta AMC}=\frac{1}{2}AM.AC.\sin\widehat{CAM}=\frac{1}{2}a.4a\frac{\sqrt{3}}{2}=a^2\sqrt{3};MC=a\sqrt{13}\)
\(\Rightarrow AE=\frac{2a\sqrt{3}}{\sqrt{13}}\)
Tính được \(AH=\frac{2a\sqrt{3}}{\sqrt{29}}\Rightarrow d\left(A,\left(CMN\right)\right)=\frac{2a\sqrt{3}}{\sqrt{29}}\Rightarrow d\left(SB,CM\right)=\frac{2a\sqrt{3}}{\sqrt{29}}\)

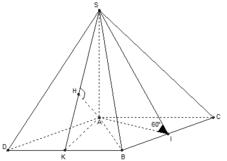
+) Hình chiếu vuông góc của SI trên mặt phẳng (ABC) là AI nên góc giữa SI và mặt phẳng (ABC) là:
(vì tam giác SIA vuông tại A nên góc SIA nhọn) ⇒ 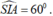
+) Xét tam giác SIA vuông tại A, 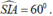
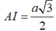 nên:
nên:
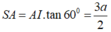
+) Dựng hình bình hành ACBD, tam giác ABC đều nên tam giác ABD đều.
+) Ta có:
AC // BD; BD ⊂ (SBD) nên AC // (SBD).
mà SB ⊂ (SBD) nên d(AC, SB) = d(A, (SBD)).
- Gọi K là trung điểm đoạn BD, tam giác ABD đều suy ra AK ⊥ BD và 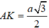 mà BD ⊥ SA nên BD ⊥ (SAK).
mà BD ⊥ SA nên BD ⊥ (SAK).
- Dựng AH ⊥ SK; H ∈ SK.
- Lại có AH ⊥ BD suy ra AH ⊥ (SBD).
- Vậy d(A, (SBD)) = AH.
- Xét tam giác SAK vuông tại vuông tại A, đường cao AH ta có:
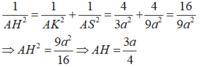
- Vậy d(AC, SB) = d(A, (SBD))
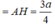
a: SA\(\perp\)(ABC)
=>SA\(\perp\)AB; SA\(\perp\)AC; SA\(\perp\)BC
=>ΔSAB vuông tại A và ΔSAC vuông tại A
Ta có: ΔABC vuông cân tại B
=>BA=BC=a và \(AC=\sqrt{AB^2+BC^2}=a\sqrt{2}\)
\(\widehat{SA;AB}=\widehat{SAB}=90^0\)
b: \(\widehat{SB;BA}=\widehat{SBA}\)
Xét ΔSAB vuông tại A có \(tanSBA=\dfrac{SA}{AB}=\dfrac{a\sqrt{2}}{a}=\sqrt{2}\)
nên \(\widehat{SBA}\simeq54^044'\)
=>\(\widehat{SB;BA}\simeq54^044'\)