Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



A B C 1 2
a) Vì AD là p/g góc A
\(\Rightarrow\widehat{A_1}=\widehat{A_2}\)
Ta có :
+) DB đối diện với góc A1
+) DC đối diện góc A2
=> DB = DC
b) Theo bài có :
AB < AC => AC - AB > 0 (1)
Theo chúng minh trên có : DB = DC
=> DB - DC = 0 (2)
Từ ( 1 ) và ( 2)
=> AC - AB > DC - DB

A B C D E
a, xét tam giác ABD và tam giác AED có AB = AE (Gt)
AD chung
^BAD = ^EAD do AD Là pg của ^BAC (Gt)
=> tg ABD = tg AED (c-g-c)
=> BD = ED (Đn)
=> tam giác BED cân tại D (đn)
b, tg ABC có AD là pg => DC/AC = DB/AB (tc)
có AC > AB (GT)
=> DC > DB
Bài làm
a) Xét tam giác ADB và tam giác ADE có:
AB = AE ( gt )
\(\widehat{BAD}=\widehat{EAD}\)( Do AD phân giác )
AD chung
=> Tam giác ADB = tam giác ADE ( c.g.c )
=> BD = DE
=> Tam giác DBE cân ở D.
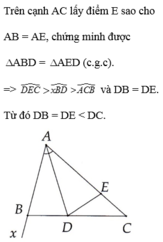
b) Kẻ BH là tia đối của tia BA.
Xét tam giác BAC có: \(\widehat{CBH}=\widehat{BAC}+\widehat{ACB}\)
=> \(\widehat{ACB}< \widehat{CBH}\)
Hay \(\widehat{DCE}< \widehat{CBH}\) (1)
Vì tam giác ADB = tam giác ADE ( cmt )
=> \(\widehat{ABD}=\widehat{AED}\)
Mà \(\widehat{ABD}+\widehat{DBH}=180^0\)( Hai góc kề bù )
\(\widehat{AED}+\widehat{DEC}=180^0\)( Hai góc kề bù )
=> \(\widehat{DBH}=\widehat{DEC}\)
Hay \(\widehat{CBH}=\widehat{DEC}\) (2)
Từ (1) và (2) => \(\widehat{DCE}< \widehat{DEC}\)
Xét tam giác DEC có:
\(\widehat{DCE}< \widehat{DEC}\)
=> DE < DC ( Qua hệ giữ cạnh và góc đối diện )
Mà DE = BD ( cmt )
=> BD < DC
Hay DC > DB ( đpcm )