Cho hình chóp S.ABCD, có đáy là hình bình hành, M và P là hai điểm lần lượt di động trên AD và SC sao cho: MA/MD = PS/PC = x (x>0). Mặt phẳng (a) đi qua M và song song với (SAB) cắt hình chóp S.ABCD theo thiết diện và cắt BD tại J.
a) Xác định x để PJ // (SAD)
b) Tính x để diện tích thiết diện bằng k lần diện tích tam giác SAB (k là số thực dương cho trước, \(k\le1\))
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tham khảo hình vẽ:
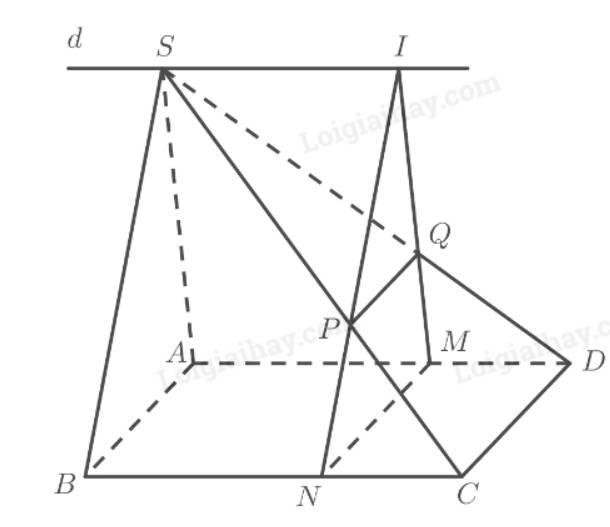
a) Ta có:
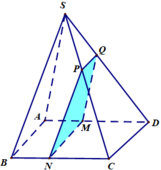
\(\begin{array}{l}MN = \left( \alpha \right) \cap \left( {ABC{\rm{D}}} \right)\\C{\rm{D}} = \left( {SC{\rm{D}}} \right) \cap \left( {ABC{\rm{D}}} \right)\\PQ = \left( \alpha \right) \cap \left( {SC{\rm{D}}} \right)\\MN\parallel C{\rm{D}}\end{array}\)
Do đó theo định lí 2 về giao tuyến của ba mặt phẳng ta có: \(MN\parallel C{\rm{D}}\parallel PQ\).
\( \Rightarrow MNPQ\) là hình bình hành.
b) Ta có:
\(\begin{array}{l}\left. \begin{array}{l}I \in MQ \Rightarrow I \in \left( {SA{\rm{D}}} \right)\\I \in NP \Rightarrow I \in \left( {SBC} \right)\end{array} \right\} \Rightarrow I \in \left( {SA{\rm{D}}} \right) \cap \left( {SBC} \right)\\ \Rightarrow SI = \left( {SA{\rm{D}}} \right) \cap \left( {SBC} \right)\\A{\rm{D}} = \left( {SA{\rm{D}}} \right) \cap \left( {ABC{\rm{D}}} \right)\\BC = \left( {SBC} \right) \cap \left( {ABC{\rm{D}}} \right)\\BC\parallel A{\rm{D}}\end{array}\)
Do đó theo định lí 2 về giao tuyến của ba mặt phẳng ta có: \(A{\rm{D}}\parallel BC\parallel SI\).
Vậy \(I\) luôn luôn thuộc đường thẳng \(d\) đi qua \(S\) song song với \(AD\) và \(BC\) cố định khi \(M\) di động trên \(AD\).

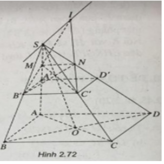
a) (P) // BC nên (P) sẽ cắt (SBC) theo giao tuyến B'C' song song với BC.
Tương tự, (P) cắt (SAD) theo giao tuyến MN song song với AD.
Khi M trùng với trung điểm A' của cạnh SA thì thiết diện MB'C'N' là hình bình hành.
b) Với M không trùng với A':
Gọi I ∈ B′M ∩ C′N. Ta có:
I ∈ B′M ⊂ (SAB), tương tự I′ ∈ C′N ⊂ (SCD)
Như vậy I ∈ Δ = (SAB) ∩ (SCD).

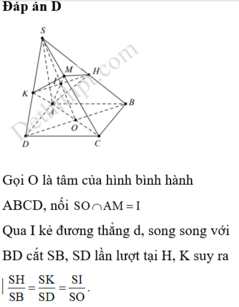
Đáp án D
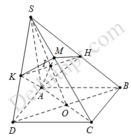
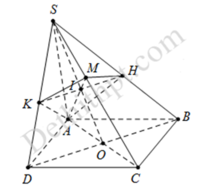
Gọi O là tâm của hình bình hành ABCD, nối S O ∩ A M = I .
Qua I kẻ đường thẳng d, song song với BD cắt SB, SD lần lượt tại H, K suy ra






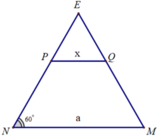


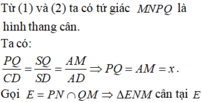
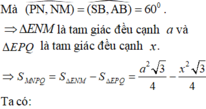
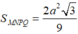
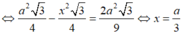
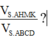

Bài này ko hề khó, đầu tiên ta dễ dàng xác định được thiết diện đi qua P theo Talet.
Gọi giao của thiết diện với BC, SD lần lượt là E, F
Để \(PJ||\left(SAD\right)\Rightarrow PJ||ME\Rightarrow PJME\) là hình bình hành (2 cặp cạnh đối song song)
\(\Rightarrow PF=MJ\)
Đến đây sử dụng tỉ lệ tam giác đồng dạng là ra x
Câu b thì từ P kẻ vuông xuống ME và S vuông xuống AB, 2 đường cao này song song theo tỉ lệ tương ứng CP/CS (Talet). Vậy là ra tỉ lệ diện tích