giải giúp mình 2 bài này nhé,mik cảm ơn (lưu ý:theo cách lớp 9 và dùng định lí Vi-et,x1x2).Cần gấp ạ:(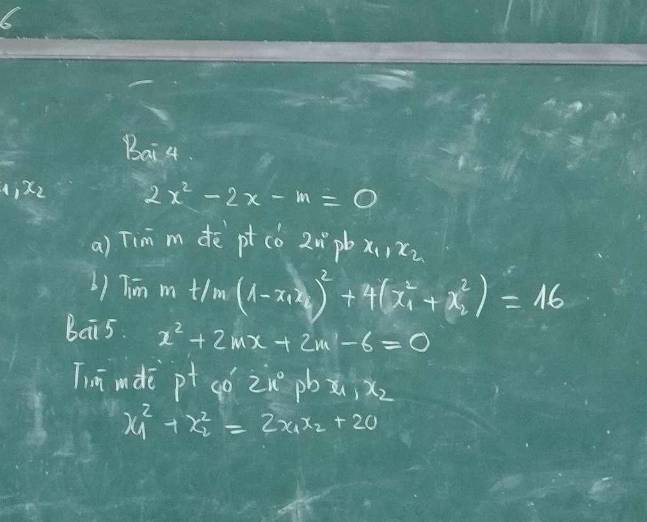
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: ΔAMN vuông tại A
mà AI là đường trung tuyến
nên AI=IM=IN=MN/2
=>I là tâm đường tròn ngoại tiếp ΔAMN
b: Xét (O) có
ΔBAC nội tiếp
BC là đường kính
Do đó: ΔBAC vuông tại A
Xét (O) có
ΔBEC nội tiếp
BC là đường kính
Do đó: ΔBEC vuông tại E

IX
2. j
3. i
4. f
5. c
6. a
7. h
8. e
9. g
10. d
XI
2. part => parts
3. a => an
4. a => an
5. a => the
6. are => will be (không chắc lắm)
7. taking => take
8. are => is
C.
Bài 1
1. C
2. B
3. C
4. B
(Nên double-check trước khi chép)

3.
\(\Delta'=\left(m-1\right)^2-\left(-2m-1\right)=m^2+2>0;\forall m\)
\(\Rightarrow\) Pt luôn có 2 nghiệm pb với mọi m
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2\left(m-1\right)\\x_1x_2=-2m-1\end{matrix}\right.\)
\(2x_1+3x_2+3x_1x_2=-11\)
\(\Leftrightarrow2\left(x_1+x_2\right)+x_2+3x_1x_2=-11\)
\(\Leftrightarrow4\left(m-1\right)+x_2+3\left(-2m-1\right)=-11\)
\(\Leftrightarrow x_2=2m-4\)
Thế vào \(x_1+x_2=2\left(m-1\right)\)
\(\Rightarrow x_1=2\left(m-1\right)-\left(2m-4\right)=2\)
Thế \(x_1=2;x_2=2m-4\) vào \(x_1x_2=-2m-1\)
\(\Rightarrow2\left(2m-4\right)=-2m-1\)
\(\Rightarrow m=\dfrac{7}{6}\)
4.
\(\Delta'=\left(m+1\right)^2-\left(m^2-m-5\right)=3m+6>0\Rightarrow m>-2\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-2\left(m+1\right)\\x_1x_2=m^2-m-5\end{matrix}\right.\)
Do \(x_1\) là nghiệm của pt nên:
\(x_1^2+2\left(m+1\right)x_1+m^2-m-5=0\)
\(\Rightarrow x_1^2=-2\left(m+1\right)x_1-m^2+m+5\)
Từ đó ta được:
\(x_1^2-2\left(m+1\right)x_2+m^2-m-5=16\)
\(\Leftrightarrow-2\left(m+1\right)x_1-m^2+m-5-2\left(m+1\right)x_2+m^2-m-5=16\)
\(\Leftrightarrow-2\left(m+1\right)\left(x_1+x_2\right)=16\)
\(\Leftrightarrow4\left(m+1\right)^2=16\)
\(\Leftrightarrow\left(m+1\right)^2=4\)
\(\Rightarrow\left[{}\begin{matrix}m+1=2\\m+1=-2\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}m=1\\m=-3< -2\left(loại\right)\end{matrix}\right.\)

#include <bits/stdc++.h>
using namespace std;
double a,cv,dt;
int main()
{
cin>>a;
cv=a*4;
dt=a*a;
cout<<fixed<<setprecision(2)<<cv<<endl;
cout<<fixed<<setprecision(2)<<dt;
return 0;
}

Do you use solar energy in your home?
People won't use flying cars until the year 2050
We must always obey the traffic rules for our safety
The major cause of death for children living in the slums is malnutrition
Solar panels will be installed on the roof of our house next week
Veronica is a good friend of mine
Pollution is the most serious problem

2\(\sqrt{\dfrac{16}{3}}\) - 3\(\sqrt{\dfrac{1}{27}}\) - \(\dfrac{3}{2\sqrt{3}}\)
= \(\dfrac{8}{\sqrt{3}}\) - \(\dfrac{3}{3\sqrt{3}}\) - \(\dfrac{3}{2\sqrt{3}}\)
= \(\dfrac{8}{\sqrt{3}}\) - \(\dfrac{1}{\sqrt{3}}\) - \(\dfrac{3}{2\sqrt{3}}\)
= \(\dfrac{16}{2\sqrt{3}}\) - \(\dfrac{2}{2\sqrt{3}}\) - \(\dfrac{3}{2\sqrt{3}}\)
= \(\dfrac{11}{2\sqrt{3}}\)
= \(\dfrac{11\sqrt{3}}{6}\)
f, 2\(\sqrt{\dfrac{1}{2}}\)- \(\dfrac{2}{\sqrt{2}}\) + \(\dfrac{5}{2\sqrt{2}}\)
= \(\dfrac{2}{\sqrt{2}}\) - \(\dfrac{2}{\sqrt{2}}\) + \(\dfrac{5}{2\sqrt{2}}\)
= \(\dfrac{5}{2\sqrt{2}}\)
= \(\dfrac{5\sqrt{2}}{4}\)
(1 + \(\dfrac{3-\sqrt{3}}{\sqrt{3}-1}\)).(1- \(\dfrac{3+\sqrt{3}}{\sqrt{3}+1}\))
= \(\dfrac{\sqrt{3}-1+3-\sqrt{3}}{\sqrt{3}-1}\).\(\dfrac{\sqrt{3}+1-3+\sqrt{3}}{\sqrt{3}+1}\)
= \(\dfrac{2}{\sqrt{3}-1}\).\(\dfrac{-2}{\sqrt{3}+1}\)
= \(\dfrac{-4}{3-1}\)
= \(\dfrac{-4}{2}\)
= -2

Bài 3:
a. \(R=R1+R2=15+30=45\Omega\)
b. \(\left\{{}\begin{matrix}I=U:R=9:45=0,2A\\I=I1=I2=0,2A\left(R1ntR2\right)\end{matrix}\right.\)
c. \(\left\{{}\begin{matrix}U1=R1.I1=15.0,2=3V\\U2=R2.I2=30.0,2=6V\end{matrix}\right.\)
Bài 4:
\(I1=U1:R1=6:3=2A\)
\(\Rightarrow I=I1=I2=2A\left(R1ntR2\right)\)
\(U=R.I=\left(3+15\right).2=36V\)
\(U2=R2.I2=15.2=30V\)
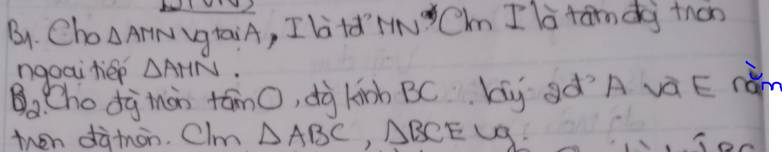


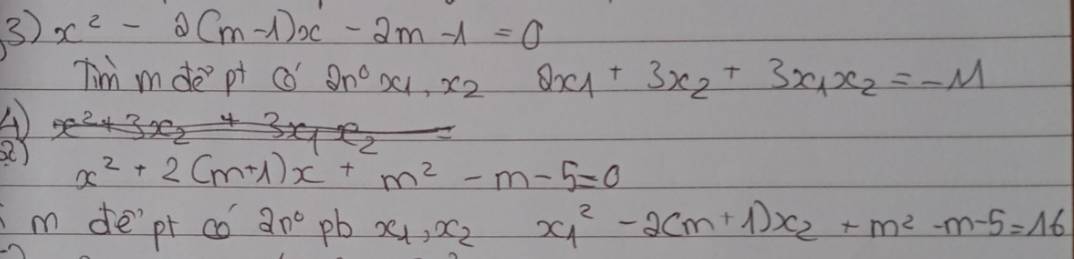

 giúp mình bài này với. Mình cần gấp ấy, mik cảm ơn các bạn nhé.
giúp mình bài này với. Mình cần gấp ấy, mik cảm ơn các bạn nhé.


Bài 5:
\(x^2+2mx+2m-6=0\)
\(\text{Δ}=\left(2m\right)^2-4\left(2m-6\right)\)
\(=4m^2-8m+24\)
\(=4m^2-8m+4+20\)
\(=\left(2m-2\right)^2+20>=20>0\forall m\)
=>Phương trình luôn có hai nghiệm phân biệt
Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=\dfrac{-2m}{1}=-2m\\x_1x_2=\dfrac{c}{a}=\dfrac{2m-6}{1}=2m-6\end{matrix}\right.\)
\(x_1^2+x_2^2=2x_1x_2+20\)
=>\(\left(x_1+x_2\right)^2-2x_1x_2-2x_1x_2=20\)
=>\(\left(-2m\right)^2-4\left(2m-6\right)=20\)
=>\(4m^2-8m+24-20=0\)
=>\(4m^2-8m+4=0\)
=>\(\left(2m-2\right)^2=0\)
=>2m-2=0
=>2m=2
=>m=1(nhận)
Câu 4:
a: \(2x^2-2x-m=0\)
\(\text{Δ}=\left(-2\right)^2-4\cdot2\cdot\left(-m\right)\)
\(=4+8m\)
Để phương trình có hai nghiệm phân biệt thì 8m+4>0
=>8m>-4
=>\(m>-\dfrac{1}{2}\)
b: Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{-b}{a}=\dfrac{-\left(-2\right)}{2}=\dfrac{2}{2}=1\\x_1x_2=\dfrac{c}{a}=\dfrac{-m}{2}\end{matrix}\right.\)
\(\left(1-x_1x_2\right)^2+4\cdot\left(x_1^2+x_2^2\right)=16\)
=>\(\left(1+\dfrac{m}{2}\right)^2+4\cdot\left[\left(x_1+x_2\right)^2-2x_1x_2\right]=16\)
=>\(\left(\dfrac{m+2}{2}\right)^2+4\left[1^2-2\cdot\dfrac{-m}{2}\right]=16\)
=>\(\dfrac{1}{4}\left(m^2+4m+4\right)+4\left(1+m\right)=16\)
=>\(\dfrac{1}{4}m^2+m+1+4+4m-16=0\)
=>\(\dfrac{1}{4}m^2+5m-11=0\)
=>\(m^2+20m-44=0\)
=>(m+22)(m-2)=0
=>\(\left[{}\begin{matrix}m+22=0\\m-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=-22\left(loại\right)\\m=2\left(nhận\right)\end{matrix}\right.\)
5.
\(\Delta'=1+2m\)
a.
Phương trình có 2 nghiệm pb khi:
\(1+2m>0\Rightarrow m>-\dfrac{1}{2}\)
b.
Khi pt có 2 nghiệm, theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=1\\x_1x_2=-\dfrac{m}{2}\end{matrix}\right.\)
\(\left(1-x_1x_2\right)^2+4\left(x_1^2+x_2^2\right)=16\)
\(\Leftrightarrow\left(1-x_1x_2\right)^2+4\left(x_1+x_2\right)^2-8x_1x_2=16\)
\(\Leftrightarrow\left(1+\dfrac{m}{2}\right)^2+4.1^2+4m=16\)
\(\Leftrightarrow\dfrac{m^2}{4}+5m-11=0\Rightarrow\left[{}\begin{matrix}m=2\\m=-22< -\dfrac{1}{2}\left(loại\right)\end{matrix}\right.\)
5.
\(\Delta'=m^2-\left(2m-6\right)=\left(m-1\right)^2+5>0;\forall m\)
Pt luôn có 2 nghiệm pb
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-2m\\x_1x_2=2m-6\end{matrix}\right.\)
\(x_1^2+x_2^2=2x_1x_2+20\)
\(\Leftrightarrow\left(x_1+x_2\right)^2=4x_1x_2+20\)
\(\Leftrightarrow4m^2=4\left(2m-6\right)+20\)
\(\Leftrightarrow m^2-2m+1=0\Rightarrow m=1\)