Chứng minh rằng: nếu có các số x;y;z;t thõa mãn đẳng thức :[xy(xy-2zt)+z2.t2].[xy(xy-z)-z.(xy+1)]=0
thì nó lập thành 1 tỉ lệ thức
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KK
1
24 tháng 3 2020
vì x,y là các số dương =>x,y>0
ta có x>y(gt)=>x^2>xy
mà xy >y^2 ( vì x>y) =>x^2>y^2
vì x,y >0 và x^2>y^2 =>căn x^2 > căn y^2 => x>y (đpcm)
CM
8 tháng 4 2019
Hàm số:
f
x
=
-
2
x
nếu
x
≥
0
sin
x
2
nếu
x
<
0
Không có đạo hàm tại x = 0 vì:
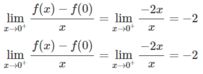
Mặt khác, với x < 0 thì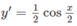 
với x > 0 thì y’ = -2 < 0
Bảng biến thiên:
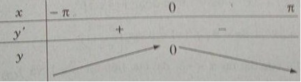
Từ đó ta thấy hàm số đạt cực đại tại x = 0 và y CD = y(0) = 0.
31 tháng 10 2019
Ta thấy tổng các chữ số của số 2004 là 6 nên 2004 chia hết cho 3
mà không chia hết 9
nên số có tổng các chữ số là 2004 cũng chia hết cho 3 mà không chia hết cho 9,
do đó số này không phải là số chính phương.
31 tháng 10 2019
Vì số chính phương khi chia cho 3 chỉ có số dư là 0 hoặc 1 . Do tổng các chữ số của số đó là 2004 nên số đó chia hết cho 3. Chứng tỏ số đã cho là số chính phương.
vậy số đã cho có tổng các chưa số là 2004 là một số chính phương