giải chi tiết giùm mik nhé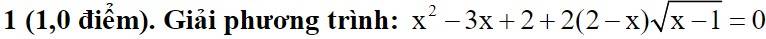
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DT
5
KC
27 tháng 12 2018
38+(-135)-38 = 38 - 135 - 38 = ( 38 - 38 ) - 135 = 0 - 135 = -135
27 tháng 12 2018
38+(-135)-38=(38-38)+(-135)=0+(-135)=-135
4 tháng 10 2016
SBC + SC + SD = 595
SBC + SC + 49 = 595
SBC + SC = 595 - 49
SBC + SC = 546
- Vì SBC gấp 6 lần SC & thêm 49 đ.vị => nếu SBC chỉ gấp 6 lần SC thì tổng của SBC & SC = 546 - 49 = 497
- Vì SBC gấp 6 lần SC nên ta nói SC = \(\frac{1}{6}\)SBC
Tổng số phần = nhau là :
1 + 6 = 7 ( phần )
SC là :
497 : 7 = 71
SBC là :
71 x 6 + 49 = 475
Đ/s: SC : 71
SBC : 475
S
4 tháng 10 2016
Tổng của số bị chia và số chia là:
595 - 49 = 546
VÌ khi ta lấy số bị chia phải có dư thì mới có số dư ,và thương bằng 6 thì số bị chia có 6 phần , số chia có 1 phần . Ta có sơ đồ:
SBC : !____!____!____!____!____!__49__! Tổng : 595
SC : !____!
Vậy số chia là:
(595 - 49) : (6 + 1) = 78
Số bị chia là:
78 x 6 + 49 = 517
NK
15 tháng 12 2021
2)
a)
chiều dài ADN: L=N/2*3.4=5100A
chu kì vòng xoắn: c=N/20=150
b)
Nu loại A chiếm 20%=> A=T=3000.20%=600
từ Nu loại A = 20%=> Nu loại G= 30%=> G=X=900
số lk H= 2A+3G= 2*600+3*900=3900
PT
3
20 tháng 10 2019
Nhận thấy 9^9 là số lẻ => 9^9 =2k+1 (k là stn)
Xét 9^9^9 =9^2k+1 =9^2k *9 =81^k *9 =...1 *9 =...9
Vậy 9^9^9 tận cùng là 9
20 tháng 10 2019
Ta có \(9^{9^9}=9^{\left(9^2\right)^4.9}=9^{81^4.9}=9^{\left(\overline{...1}\right).9}=9^{\overline{...9}}=9^{\overline{...8}}.9=\left(9^2\right)^{...}.9\)(tách (...8)=2.(...) (... là số ko biết c/s tận cùng)
\(\left(81\right)^{...}.9=\left(\overline{...1}\right).9=\overline{...9}\)
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 1 2022
Số hạng đó là số hạng thứ 4 \(\Rightarrow k=3\) nên có dạng:
\(C_6^3\left(2x\right)^3.\left(-y^2\right)^3=-C_6^3\left(2x\right)^3y^6\)
5 tháng 11 2017
2 , 5 - x = 1 , 3
x = 2 , 5 - 1 , 3
x = 1 , 2
Chúc bạn chăm ngoan học giỏi !
LV
1
17 tháng 10 2021
c: \(\dfrac{1}{8}x^3-\dfrac{9}{4}x^2y+\dfrac{27}{2}xy^2-27y^3=\left(\dfrac{1}{2}x-3y\right)^3\)
b: \(-x^3+12x^2-48x+64=\left(-x+4\right)^3\)
\(x^2+3x+2+2\left(2-x\right)\sqrt{x-1}=0\left(x\ge1\right)\)
\(\Leftrightarrow x^2-x-2x+2-2\left(x-2\right)\sqrt{x-1}=0\)
\(\Leftrightarrow x\left(x-1\right)-2\left(x-1\right)-2\left(x-2\right)\sqrt{x-1}=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-2\right)-2\left(x-2\right)\sqrt{x-1}=0\)
\(\Leftrightarrow\left(x-2\right)\sqrt{x-1}\left(\sqrt{x-1}-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=0\\\sqrt{x-1}=0\\\sqrt{x-1}-2=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\left(tm\right)\\x-1=0\\\sqrt{x-1}=2\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\left(tm\right)\\x=1\left(tm\right)\\x-1=4\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=1\\x=5\end{matrix}\right.\left(tm\right)\)
Vậy: \(x\in\left\{1;2;5\right\}\)