Chứng minh biểu thức luôn dương:
a)4x2-2x+1
b)x4-3x2+9
c)x2+y2-2x-2y+2xy+2
d)x23xy+3y2 với x,y khác 0
e)2x2+y2+2x.(y-1)+2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Có hai cách trình bày với bài này: một là bạn có thể liệt kê hết các phần tử ra hoặc bạn sắp xếp theo cùng thứ tự và tính như sau:


e) Ta có: \(x^4-2x^3+2x-1\)
\(=\left(x^4-1\right)-2x\left(x^2-1\right)\)
\(=\left(x^2+1\right)\left(x-1\right)\left(x+1\right)-2x\left(x-1\right)\left(x+1\right)\)
\(=\left(x-1\right)\left(x+1\right)\cdot\left(x^2-2x+1\right)\)
\(=\left(x+1\right)\cdot\left(x-1\right)^3\)
h) Ta có: \(3x^2-3y^2-2\left(x-y\right)^2\)
\(=3\left(x^2-y^2\right)-2\left(x-y\right)^2\)
\(=3\left(x-y\right)\left(x+y\right)-2\left(x-y\right)^2\)
\(=\left(x-y\right)\left(3x+3y-2x+2y\right)\)
\(=\left(x-y\right)\left(x+5y\right)\)
a) Ta có: \(x^2-y^2-2x-2y\)
\(=\left(x-y\right)\left(x+y\right)-2\left(x+y\right)\)
\(=\left(x+y\right)\left(x-y-2\right)\)
b) Ta có: \(x^2\left(x+2y\right)-x-2y\)
\(=\left(x+2y\right)\left(x^2-1\right)\)
\(=\left(x+2y\right)\left(x-1\right)\left(x+1\right)\)

a: Ta có: \(x^2-4y^2-2x-4y\)
\(=\left(x-2y\right)\left(x+2y\right)-2\left(x+2y\right)\)
\(=\left(x+2y\right)\left(x-2y-2\right)\)
c: Ta có: \(x^3+2x^2y-x-2y\)
\(=x^2\left(x+2y\right)-\left(x+2y\right)\)
\(=\left(x+2y\right)\left(x-1\right)\left(x+1\right)\)
d: Ta có: \(3x^2-3y^2-2\cdot\left(x-y\right)^2\)
\(=3\left(x-y\right)\left(x+y\right)-2\cdot\left(x-y\right)^2\)
\(=\left(x-y\right)\left(3x+3y-2x+2y\right)\)
\(=\left(x-y\right)\left(x+5y\right)\)
e: Ta có: \(x^3-4x^2-9x+36\)
\(=x^2\left(x-4\right)-9\left(x-4\right)\)
\(=\left(x-4\right)\left(x-3\right)\left(x+3\right)\)
f: Ta có: \(x^2-y^2-2x-2y\)
\(=\left(x-y\right)\left(x+y\right)-2\left(x+y\right)\)
\(=\left(x+y\right)\left(x-y-2\right)\)

a: \(\left(2x-1\right)^2-2\left(2x-3\right)^2+4\)
\(=4x^2-4x+1+4-2\left(4x^2-12x+9\right)\)
\(=4x^2-4x+5-8x^2+24x-18\)
\(=-4x^2+20x-13\)
e: \(\left(2x+3y\right)\left(4x^2-6xy+9y^2\right)=8x^3+27y^3\)

Bài \(3\)
\(A=\left(x-5\right)\left(2x+3\right)-2x\left(x-3\right)+x+7\)
\(=2x^2+3x-10x-15-\left(2x^2-6x\right)+x+7\)
\(=2x^2+3x-10x-15-2x^2+6x+x+7\)
\(=\left(2x^2-2x^2\right)+\left(3x-10x+6x+x\right)+\left(-15+7\right)\)
\(=-8\)
Vậy biểu thức không phụ thuộc vào biến
\(B=4\left(y-6\right)-y^2\left(2+3y\right)+y\left(5y-4\right)+3y^2\)
Đề như này à?
Bài \(4\)
\(a,4a^2-16b^2=4\left(a^2-4b^2\right)=4\left(a-2b\right)\left(a+2b\right)\)
\(b,4x^2-4x+1=\left(2x\right)^2-2.2x.1+1^2=\left(2x+1\right)^2\)
\(c,\) ?
\(d,\left(x-y\right)^2-\left(2x-y\right)^2\\ =\left[\left(x-y\right)-\left(2x-y\right)\right]\left[\left(x-y\right)+\left(2x-y\right)\right]\\ =\left(x-y-2x+y\right)\left(x-y+2x-y\right)\\ =\left(-x\right)\left(3x-2y\right)\)
\(e,8x^3-y^3=\left(2x\right)^3-y^3\\ =\left(2x-y\right)\left(4x^2+2xy+y^2\right)\)
\(i,3x+6y+\left(x+2y\right)\\ =3\left(x+2y\right)+\left(x+2y\right)\\ =4\left(x+2y\right)\)
\(j,ax-ay-x+y=\left(ãx-ay\right)-\left(x-y\right)\\ =a\left(x-y\right)-\left(x-y\right)=\left(x-y\right)\left(a-1\right)\)
`k,` `y` hay `y^2` ạ? vì nó mới phân tích được nhân tử.

a.
$x^2-y^2-2x+2y=(x^2-y^2)-(2x-2y)=(x-y)(x+y)-2(x-y)=(x-y)(x+y-2)$
b.
$x^2(x-1)+16(1-x)=x^2(x-1)-16(x-1)=(x-1)(x^2-16)=(x-1)(x-4)(x+4)$
c.
$x^2+4x-y^2+4=(x^2+4x+4)-y^2=(x+2)^2-y^2=(x+2-y)(x+2+y)$
d.
$x^3-3x^2-3x+1=(x^3+1)-(3x^2+3x)=(x+1)(x^2-x+1)-3x(x+1)$
$=(x+1)(x^2-4x+1)$
e.
$x^4+4y^4=(x^2)^2+(2y^2)^2+2.x^2.2y^2-4x^2y^2$
$=(x^2+2y^2)^2-(2xy)^2=(x^2+2y^2-2xy)(x^2+2y^2+2xy)$
f.
$x^4-13x^2+36=(x^4-4x^2)-(9x^2-36)$
$=x^2(x^2-4)-9(x^2-4)=(x^2-9)(x^2-4)=(x-3)(x+3)(x-2)(x+2)$
g.
$(x^2+x)^2+4x^2+4x-12=(x^2+x)^2+4(x^2+x)-12$
$=(x^2+x)^2-2(x^2+x)+6(x^2+x)-12$
$=(x^2+x)(x^2+x-2)+6(x^2+x-2)=(x^2+x-2)(x^2+x+6)$
$=[x(x-1)+2(x-1)](x^2+x+6)=(x-1)(x+2)(x^2+x+6)$
h.
$x^6+2x^5+x^4-2x^3-2x^2+1$
$=(x^6+2x^5+x^4)-(2x^3+2x^2)+1$
$=(x^3+x^2)^2-2(x^3+x^2)+1=(x^3+x^2-1)^2$

a: Ta có: \(\left(2x-1\right)^2-2\left(2x-3\right)^2+4\)
\(=4x^2-4x+1-2\left(4x^2-12x+9\right)+4\)
\(=4x^2-4x+5-8x^2+24x-18\)
\(=-4x^2+20x-13\)
b: \(\left(3x+2\right)^2+2\left(3x+2\right)\left(1-2y\right)+\left(1-2y\right)^2\)
\(=\left(3x+2+1-2y\right)^2\)
\(=\left(3x-2y+3\right)^2\)

Bài 4
c) x(x - 2) + (x - 2)²
= (x - 2)(x + x - 2)
= (x - 2)(2x - 2)
= 2(x - 2)(x - 1)
d) 2x(x - y)² - 5(y - x)
= 2x(x - y)² + 5(x - y)
= (x - y)(2x + 5)
Bài 5
a) x² - 6x - 2xy + 12y
= (x² - 6x) - (2xy - 12y)
= x(x - 6) - y(x - 6)
= (x - 6)(x - y)
b) 10ax - 5ay - 2x + y
= (10ax - 5ay) - (2x - y)
= 5a(2x - y) - (2x - y)
= (2x - y)(5a - 1)
c) x⁴ + x³y - x - y
= (x⁴ + x³y) - (x + y)
= x³(x + y) - (x + y)
= (x + y)(x³ - 1)
= (x + y)(x - 1)(x² + x + 1)
d) x³ + 2x² - 4x - 8
= (x³ + 2x²) - (4x + 8)
= x²(x + 2) - 4(x + 2)
= (x + 2)(x² - 4)
= (x + 2)(x + 2)(x - 2)
= (x + 2)²(x - 2)
e) xy - 5x - y² + 5y
= (xy - 5x) - (y² - 5y)
= x(y - 5) - y(y - 5)
= (y - 5)(x - y)
f) ax - bx - 2cx - 2a + 2b + 4c
= (ax - bx - 2cx) - (2a - 2b - 4c)
= x(a - b - 2c) - 2(a - b - 2c)
= (a - b - 2c)(x - 2)
g) 5x²y + 5xy² - b²x - b²y
= (5x²y + 5xy²) - (b²x + b²y)
= 5xy(x + y) - b²(x + y)
= (x + y)(5xy - b²)
h) 4x³ - 4x² - 9x + 9
= (4x³ - 4x²) - (9x - 9)
= 4x²(x - 1) - 9(x - 1)
= (x - 1)(4x² - 9)
= (x - 1)(2x - 3)(2x + 3)
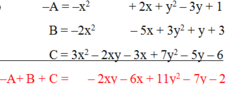
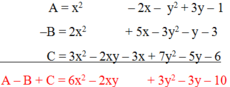
a, Ta có: 4x2-2x+1 = (x2 -2x+1)+ 3x2=(x-1)2 +3x2>0 (thay x=1 và x=0 thì biểu thức vãn lớn hơn 0)
b, x4-3x2+9=x4- 6x2 +32 +3x2=(x2-3)2 +3x2 >0
c, x2+y2-2x-2y+2xy+2=(x+y)2 -1 -2(x+y-1) +1 =(x+y -1)(x+y+1) - 2(x+y-1)+1=(x+y-1)(x+y+1-2) + 1=(x+y-1)2 +1 >0
d, 2(x2+3xy+3y2)=2x2+6xy+6y2=(x2+2xy+y2) +(x2+4xy+4y2)+y2=(x+y)2+(x+2y)2+y2>0
e, 2x2+y2+2x(y-1)+2= (x2+2xy+y2) +(x2-2x+1)+1=(x+y)2+(x-1)+1>0
nhớ bấm đúng cho mình nhé!