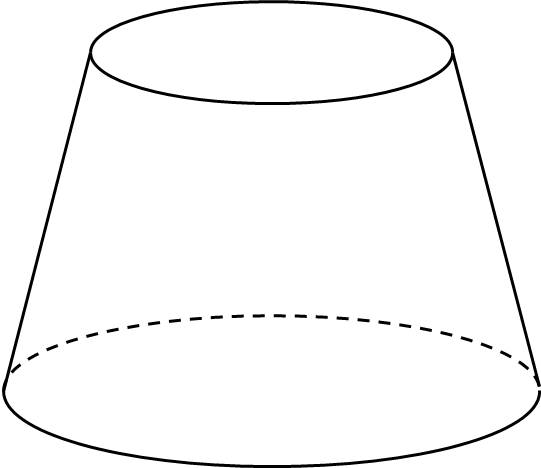
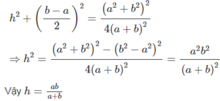Vẽ các hình chiếu vuông góc của:
a) Hình chóp cụt tứ giác đều.
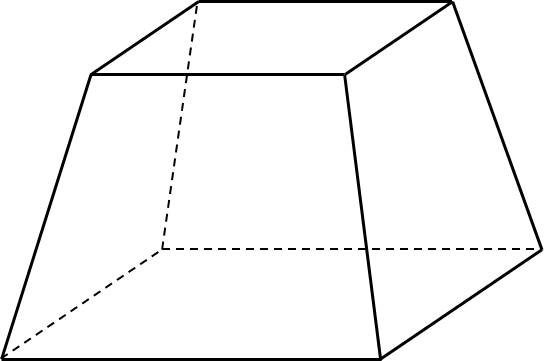
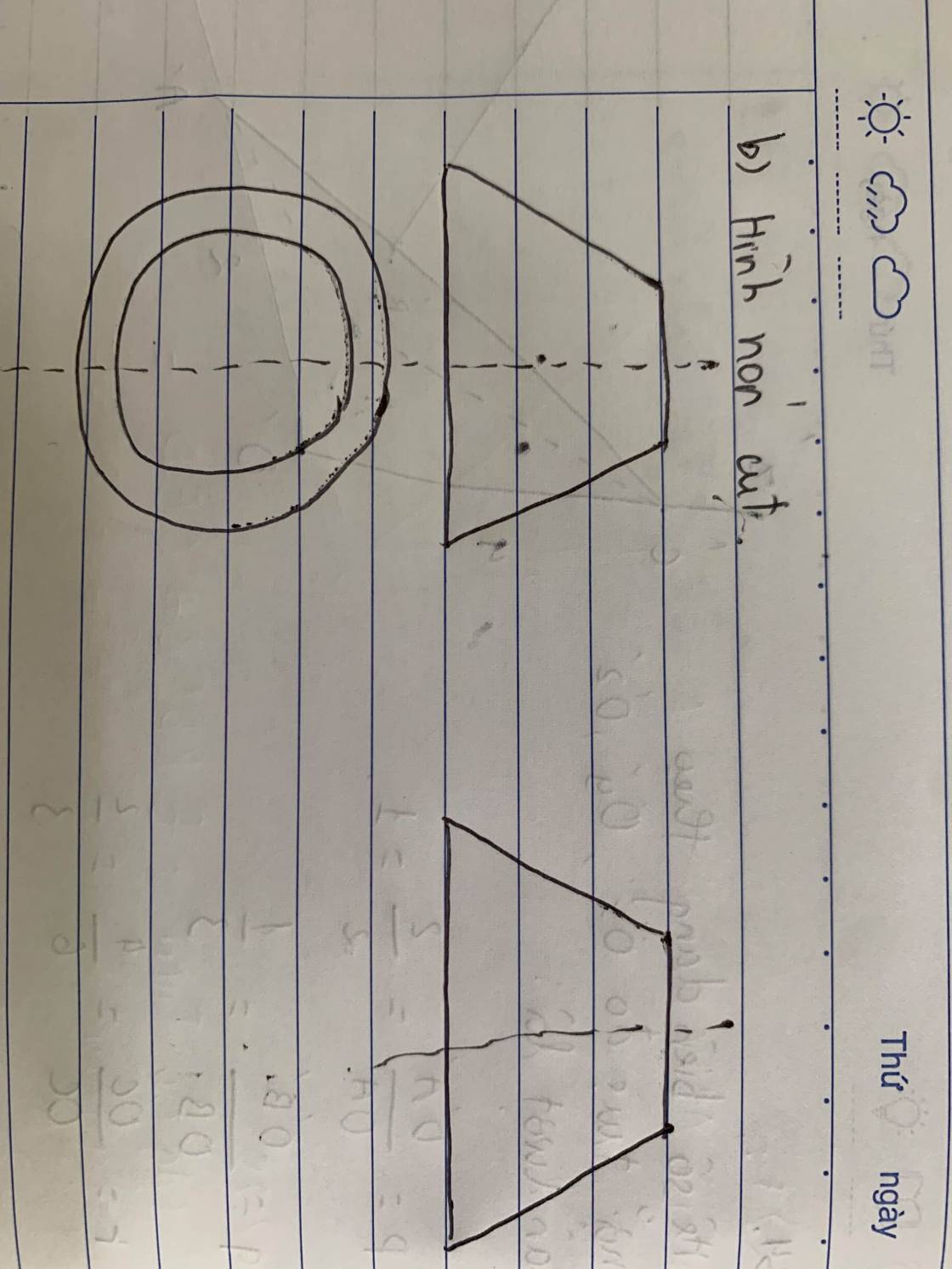
b) Hình nón cụt.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

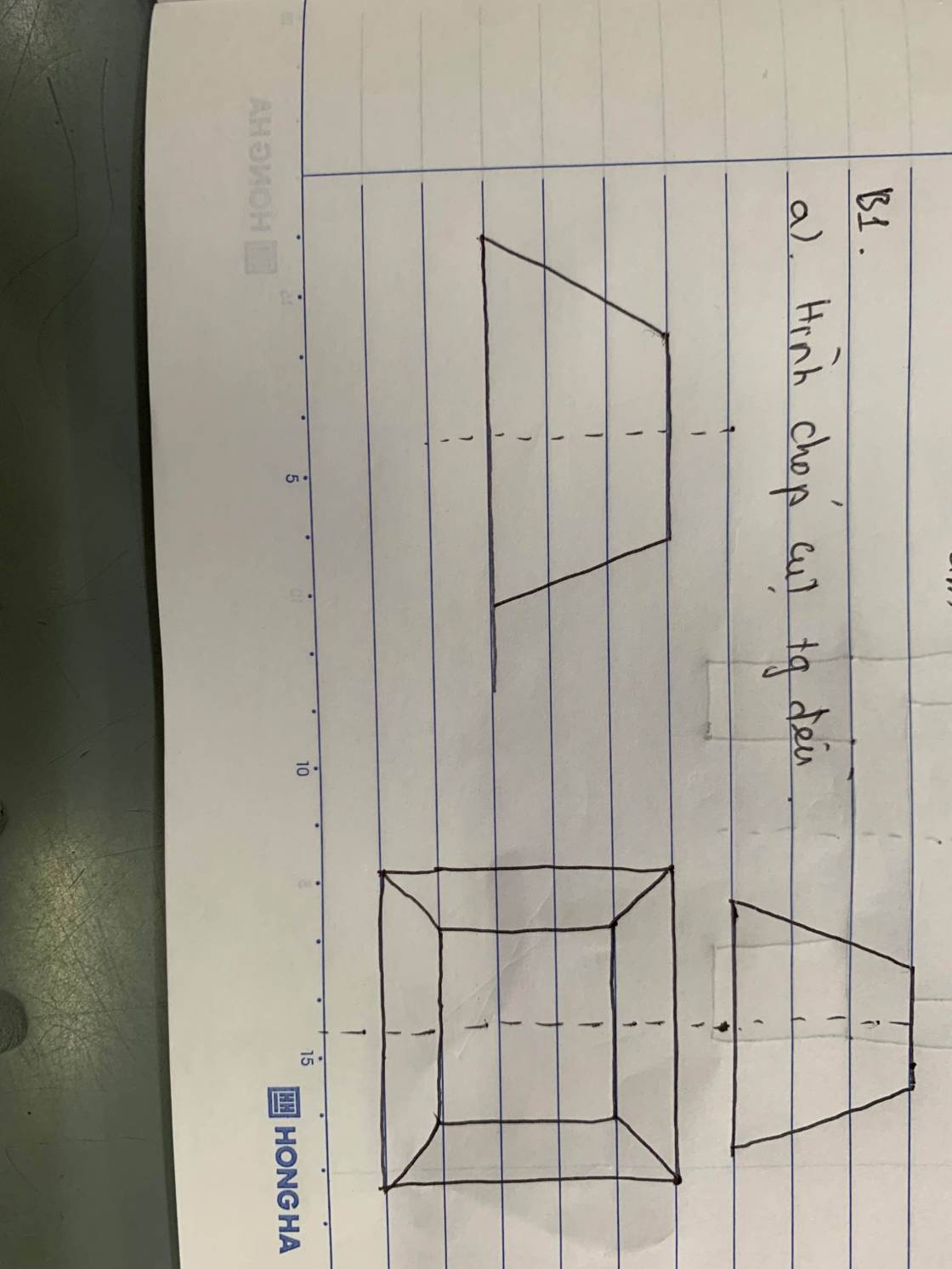

\(a,S_{xp}=4.\dfrac{a+2a}{2}.a=6a^2\)
\(b,\)Vẽ một mặt bên. Ta có:\(AH=\dfrac{AB-A^'B^'}{2}=\dfrac{2a-a}{2}=\dfrac{a}{2}\)
Trong tamn giác vuông A'HA:
\(AA^'=\sqrt{a^2+\left(\dfrac{a}{2}\right)^2}=\sqrt{\dfrac{5a^2}{4}}\)
Từ đó tính tiếp sẽ ra chiều cao hình chóp
Đáp số :Độ dài cạnh bên là :\(\sqrt{\dfrac{5a^2}{4}}\)
Chiều cao chóp cụt :\(\sqrt{\dfrac{3a^2}{4}}\)

Diện rích một mặt bên là hình thang bằng:
S =1/2 (5 +10).5=37,5 ( c m 2 )
Diện tích xung quanh của hình chóp
cụt đều là: S x q =4.3,75 = 150 ( c m 2 )

1. Phương pháp biểu diễn các hình chiếu vuông góc trên cùng một mặt phẳng hình chiếu gọi là phương pháp hình chiếu vuông góc. Có 2 phương pháp chiếu: Phương pháp chiếu góc thứ nhất và phương pháp chiếu góc thứ ba.
2.
- Hình hộp chữ nhật: được bao bởi 2 mặt đáy là hình chữ nhật bằng nhau và 4 mặt bên là các hình chữ nhật.
- Hình lăng trụ tam giác đều: được bao bởi 2 mặt đáy là hình tam giác đều bằng nhau và 3 mặt bên là các hình chữ nhật.
- Hình chóp tứ giác đều: được bao bởi mặt đáy là hình vuông và 4 mặt bên là các hình tam giác đều bằng nhau.
- Hình trụ: có hình chiếu đứng và hình chiếu cạnh là hình chữ nhật; hình chiếu bằng là hình tròn
- Hình nón: có hình chiếu đứng và hình chiếu cạnh là hình tam giác, hình chiếu bằng là hình tròn.
- Hình cầu: cả ba hình chiếu đứng, bằng, cạnh là hình tròn có cùng đường kính.
3.
Đối với khối đa diện đều, cần 3 hình chiếu để đủ biểu diễn hình dạng và kích thước
4.
Các bước vẽ hình chiếu vuông góc của vật thể:
- Bước 1: Phân tích vật thể thành các thể khối đơn giản
- Bước 2: Chọn các hướng chiếu
- Bước 3: Vẽ các hình chiếu các bộ phận của vật thể bằng nét liền mảnh
- Bước 4: Hoàn thiện các nét vẽ và ghi kích thuớc
5.
– Gồm 5 bước:
1. Khung tên.
2. Hình biểu diễn.
3. Kích thước.
4. Yêu cầu kĩ thuật.
5. Tổng hợp.
6.
1. Khung tên
2. Bảng kê
3. Hình biểu diễn
4. Kích thước
5. Phân tích chi tiết
6. Tổng hợp

Xét hình chóp cụt đều ABCD.A'B'C'D' như hình bs.19.
Gọi M, M' thứ tự là trung điểm của BC, B'C'. Khi đó MM' là đường cao của hình thang cân BCC'B'.
Do đó diện tích xung quanh của hình chóp cụt đều là:
S x q = 4.(a+b)/2.MM′=(2a+2b).MM′
Từ giả thiết ta có:
(2a+2b).MM′=
a
2
+
b
2
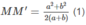
Dễ thấy OM // O'M' nên OM và O'M' xác định mặt phẳng (OMM'O'). Trong mặt phẳng (OMM'O'), kẻ MH ⊥ O'M'. Khi đó: HM' = O'M' – O'H = (b−a)/2
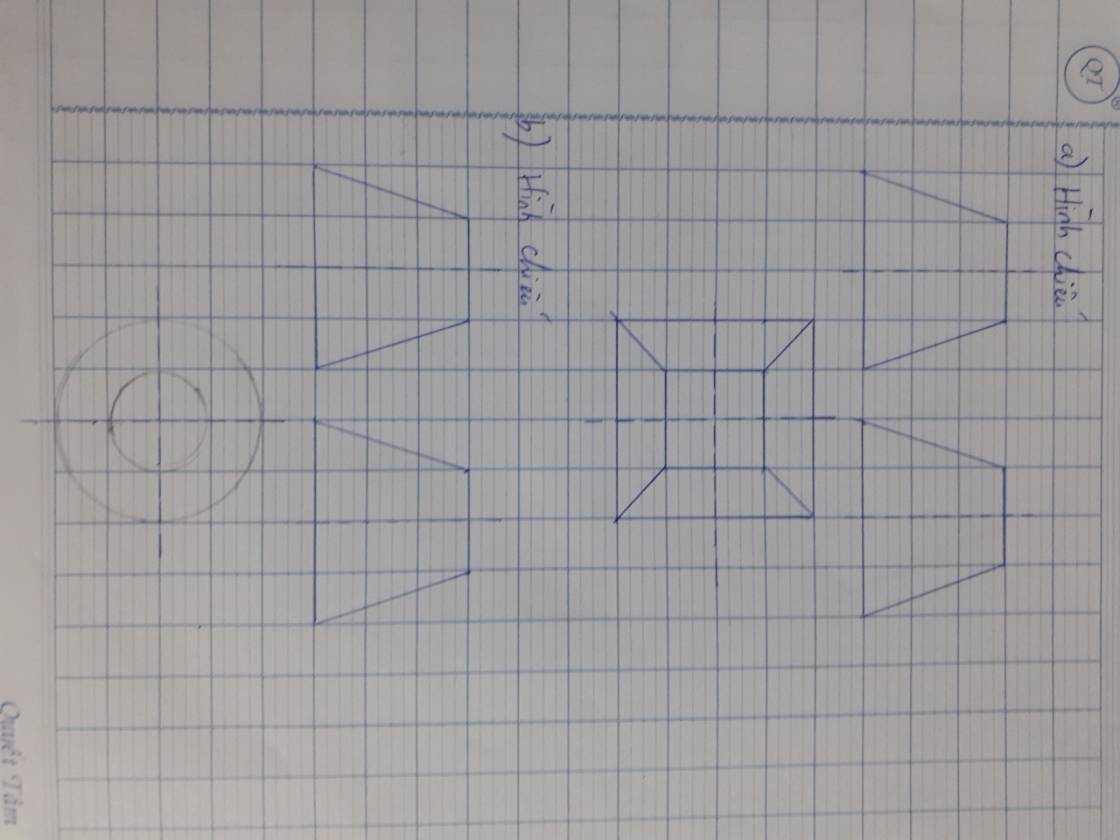
Trong tam giác vuông MHM' ta có: M M ' 2 = M H 2 + H M ' 2 = h + b - a / 2 2 (2)
Từ (1) và (2) suy ra :