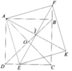
Cho hình vuông ABCD, lấy E ϵ BC, trên tia đối tia DC lấy F: BE=DF.
a) Chứng minh: AE=AF
b) Gọi M là trung điểm EF, H đối xứng với A qua M. Chứng minh AEHF là hình vuông
c) Gọi G là trọng tâm của ΔAEF. Chứng minh rằng diện tích ΔGBD không đổi khi E di chuyển trên BC