Tìm x
x2 - 3x + 2 = 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 12 2020
\(x^2+6x+9=0\\ \Leftrightarrow x^2+2.3.x+3^2=0\\ \Leftrightarrow\left(x+3\right)^2=0\\ \Leftrightarrow x+3=0\\ \Leftrightarrow x=-3\)
Vậy \(x=-3\)
CM
9 tháng 6 2019
Biểu thức xác định khi: x 2 - 4 = x + 2 x - 2 ≠ 0 và x + 2 2 ≠ 0 hay x ≠ ± 2
Ta có:
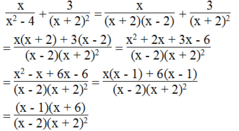
Biểu thức bằng 0 khi (x – 1)(x + 6) = 0 và x - 2 x + 2 2 ≠ 0
+) Ta có: (x - 1).(x + 6) = 0 khi x - 1= 0 hay x + 6 = 0
x - 1 = 0 khi x = 1 ( thỏa mãn điều kiện)
x + 6 = 0 khi x = -6 ( thỏa mãn điều kiện)
Vậy với x = 1 hoặc x = - 6 thì giá trị biểu thức bằng 0.
CM
23 tháng 1 2017
Biểu thức x x - 3 - x 2 + 3 x 2 x + 3 . x + 3 x 2 - 3 x - x x 2 - 9 xác định khi x – 3 ≠ 0,2x + 3 ≠ 0, x 2 - 3 x ≠ 0 và x 2 - 9 ≠ 0
Suy ra: x ≠ 3; x ≠ - 3/2 ; x ≠ 0; x ≠ 3 và x ≠ ± 3
Với điều kiện x ≠ 3; x ≠ - 3/2 ; x ≠ 0; x ≠ - 3, ta có:
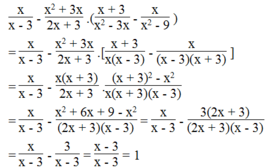
Vậy giá trị của biểu thức x x - 3 - x 2 + 3 x 2 x + 3 . x + 3 x 2 - 3 x - x x 2 - 9 bằng 1 khi x ≠ 3; x ≠ - 3/2 ; x ≠ 0; x ≠ - 3
25 tháng 2 2016
x - x * 2 + x * 2 - 2 - 3 = 0
x - 2 = 0 + 3
x - 2 = 3
x = 3 + 2
x = 5
25 tháng 2 2016
X + X x 2 + X x 2 - 2 - 3 = 0
X + X x 2 + X x 2 = 0 + 3 + 2 = 5
X x 1 + X x 2 + X x 2 = 5
X x (1 + 2 + 2) = 5
X x 5 = 5
X = 5 : 5
X = 1
CM
13 tháng 3 2019
a) (x – 1)(x2 + x + 1) – 2x = x(x – 1)(x + 1)
⇔ x3 – 1 – 2x = x(x2 – 1)
⇔ x2 – 1 – 2x = x3 – x
⇔ -2x + x = 1 ⇔ - x = 1 ⇔ x = -1
Tập nghiệm của phương trình: S = { -1}
b) x2 – 3x – 4 = 0
⇔ x2 – 4x + x – 4 = 0 ⇔ x(x – 4) + (x – 4) = 0
⇔ (x – 4)(x + 1) = 0 ⇔ x – 4 = 0 hoặc x + 1 = 0
⇔ x = 4 hoặc x = -1
Tập nghiệm của phương trình: S = {4; -1}
c) ĐKXĐ : x – 1 ≠ 0 và x2 + x + 1 ≠ 0 (khi đó : x3 – 1 = (x – 1)(x2 + x + 1) ≠ 0)
⇔ x ≠ 1
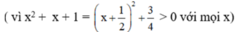
Quy đồng mẫu thức hai vế:
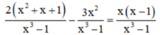
Khử mẫu, ta được: 2x2 + 2x + 2 – 3x2 = x2 – x
⇔ -2x2 + 3x + 2 = 0 ⇔ 2x2 – 3x – 2 = 0
⇔ 2x2 – 4x + x – 2 = 0 ⇔ 2x(x – 2) + (x – 2) = 0
⇔ (x – 2)(2x + 1) = 0 ⇔ x – 2 = 0 hoặc 2x + 1 = 0
⇔ x = 2 hoặc x = -1/2(thỏa mãn ĐKXĐ)
Tập nghiệm của phương trình : S = {2 ; -1/2}
d) ĐKXĐ : x – 5 ≠ 0 và x – 1 ≠ 0 (khi đó : x2 – 6x + 5 = (x – 5)(x – 1) ≠ 0)
Quy đồng mẫu thức hai vế :
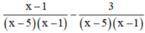
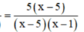
Khử mẫu, ta được : x – 1 – 3 = 5x – 25 ⇔ -4x = -21
⇔ x = 21/4 (thỏa mãn ĐKXĐ)
Tập nghiệm của phương trình : S = {21/4}
CM
12 tháng 12 2017
Đáp án A
ĐK: x < − 2 x > 2 . Ta xét f x = x 5 + x x 2 − 2 − 2017 . Có f ' x = 5 x 4 − 2 x 2 − 2 x 2 − 2 .
f ' x = 0 ⇔ 5 x 4 x 2 − 2 x 2 − 2 − 2 = 0 (*)
Xét với x < − 2 thì f x < 0 ⇒ f x = 0 không có nghiệm trong khoảng này.
Với x > 2 thì (*) có vế trai là đồng biến nên (*) chỉ có tối đa một nghiệm tức là f(x) có tối đa 2 nghiệm,
Mà f 1,45 > 0 ; f 3 0 ; f 10 0 nên f x có nghiệm thuộc 1,45 ; 3 ; 3 ; 10 từ đó f x = 0 có đúng 2 nghiệm.
\(x^2-3x+2=0\)
\(x^2-2x-x+2=0\)
\(x\left(x-2\right)-\left(x-2\right)=0\)
\(\left(x-2\right)\left(x-1\right)=0\)
=>\(x-2=0\)hoặc \(x-1=0\)
Với \(x-2=0\)=> \(x=2\)
Với \(x-1=0\)=> \(x=1\)
Vậy x=2 ; x=1
x2−3x+2=0
x2−2x−x+2=0
x(x−2)−(x−2)=0
(x−2)(x−1)=0
=>x−2=0hoặc x−1=0
Với x−2=0=> x=2
Với x−1=0=> x=1
Vậy x=2 ; x=1