Tìm nguyên hàm của y=x+1/x²+2x+2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LT
1
AH
Akai Haruma
Giáo viên
15 tháng 3 2021
Lời giải:
\(\int f(x)dx=\int \frac{x^2+2x}{x+1}dx=\int \frac{(x+1)^2-1}{x+1}dx=\int (x+1-\frac{1}{x+1})dx\)
\(=\int (x+1)dx-\int \frac{1}{x+1}dx=\frac{x^2}{2}+x-\ln |x+1|+c\)
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 3 2022
2.
\(I=\int e^{3x}.3^xdx\)
Đặt \(\left\{{}\begin{matrix}u=3^x\\dv=e^{3x}dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=3^xln3dx\\v=\dfrac{1}{3}e^{3x}\end{matrix}\right.\)
\(\Rightarrow I=\dfrac{1}{3}e^{3x}.3^x-\dfrac{ln3}{3}\int e^{3x}.3^xdx=\dfrac{1}{3}e^{3x}.3^x-\dfrac{ln3}{3}.I\)
\(\Rightarrow\left(1+\dfrac{ln3}{3}\right)I=\dfrac{1}{3}e^{3x}.3^x\)
\(\Rightarrow I=\dfrac{1}{3+ln3}.e^{3x}.3^x+C\)
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 3 2022
1.
\(I=\int\left(2x-1\right)e^{\dfrac{1}{x}}dx=\int2x.e^{\dfrac{1}{x}}dx-\int e^{\dfrac{1}{x}}dx\)
Xét \(J=\int2x.e^{\dfrac{1}{x}}dx\)
Đặt \(\left\{{}\begin{matrix}u=e^{\dfrac{1}{x}}\\dv=2xdx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=-\dfrac{e^{\dfrac{1}{x}}}{x^2}dx\\v=x^2\end{matrix}\right.\)
\(\Rightarrow J=x^2.e^{\dfrac{1}{x}}+\int e^{\dfrac{1}{x}}dx\)
\(\Rightarrow I=x^2.e^{\dfrac{1}{x}}+C\)
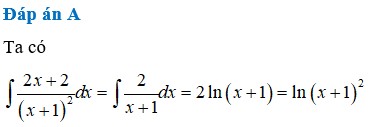
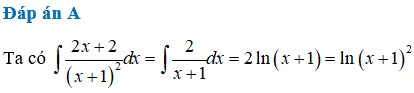
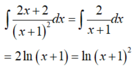
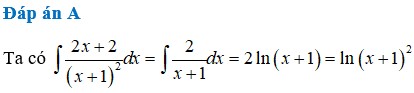
\(\int\dfrac{x+1}{x^2+2x+2}dx=\dfrac{1}{2}\int\dfrac{2x+2}{x^2+2x+2}dx=\dfrac{1}{2}\int\dfrac{d\left(x^2+2x+2\right)}{x^2+2x+2}\)
\(=\dfrac{1}{2}ln\left(x^2+2x+2\right)+C\)
Để tìm nguyên hàm của y=x+1/x²+2x+2, ta cần xác định giá trị của hàm tại một điểm nào đó.
Giá trị của hàm tại điểm nhân nguyên tố nhất là một phương án đáng tin cậy.
Trong trường hợp này, ta chọn điểm nhân nguyên tố nhất là 3.
Để tính giá trị của hàm tại điểm 3, ta đặt x=3 vào hàm y=x+1/x²+2x+2:
y=3+1/3²+2(3)+2
Ta tiến hành tính toán:
y=3+1/9+6+2
y=3+1/9+12+2
y=3+11/9+2
y=3+12/9
y=3+4/3
y=3+4
y=7
Như vậy, giá trị của hàm tại điểm 3 là 7. Do đó, nguyên hàm của y=x+1/x²+2x+2 là y=7.
Tóm lại, để tìm nguyên hàm của y=x+1/x²+2x+2, ta đã tìm được rằng giá trị của hàm tại điểm 3 là 7, do đó, nguyên hàm của y=x+1/x²+2x+2 là y=7.