Cho một lưới gồm các ô vuông. Các nút được đánh số từ 0 đến n theo chiều từ trái sang phải và từ 0 đến m theo chiều từ dưới lên trên. Hỏi có bao nhiêu đường đi khác nhau từ nút (0,0) đến nút (n,m) nếu chỉ cho phép đi trên các cạnh ô vuông theo chiều sang phải hoặc lên trên?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 12 2020
Không gian mẫu: \(C_{10}^3=120\)
Ta có 8 dãy số thỏa mãn đề bài: (0;1;9);(0;2;8);(0;3;7);(0;4;6),(1;2;7);(1;3;6);(1;4;5);(2;3;5)
Xác suất:
\(P=\dfrac{8}{120}+\left(1-\dfrac{8}{120}\right).\dfrac{8}{119}+\left(1-\dfrac{8}{120}\right).\left(1-\dfrac{8}{119}\right).\dfrac{8}{118}=...\)
CM
27 tháng 2 2017
Số cách chọn 3 nút để ấn là A 10 3 = 720 .
Số trường hợp đạt yêu cầu là: (0, 1, 9); (0, 2, 8); (0, 3, 7); (0, 4, 6); (1, 2, 7); (1, 3, 6);
(1, 4, 5) ; (2, 3, 5).
Xác xuất để B mở được cửa là 8/720 = 1/90.
CM
17 tháng 3 2018
Đáp án A
Phương pháp: Chia đường đi của thỏ thành 2 giai đoạn, tính số phần tử của không gian mẫu và số phần tử của biến cố A « thỏ đến được vị trí B » .
Cách giải :
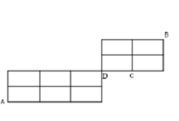
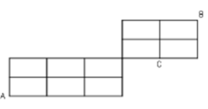
Từ A đến B nhất định phải đi qua D,
ta chia làm 2 giai đoạn A → D
CM
1 tháng 2 2018
Phương pháp: Chia đường đi của thỏ thành 2 giai đoạn, tính số phần tử của không gian mẫu và số phần tử của biến cố A « thỏ đến được vị trí B » .
Cách giải :
Từ A đến B nhất định phải đi qua D, ta chia làm 2 giai đoạn A → D và D → B
Từ A → D có 9 cách.
Từ D → B có 6 cách tính cả đi qua C và có 3 cách không đi qua C.
Không gian mẫu n Ω = 9 . 6 = 54
Gọi A là biến cố « thỏ đến được vị trí B » thì nA = 9.3 = 27
Vậy
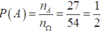
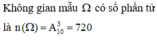
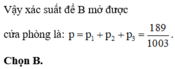
Để đi từ điểm tọa độ (0,0) đến tọa độ (n,m) thì cần n bước qua phải và m bước lên trên, nên cần tổng cộng \(m+n\) bước đi để đến đích.
Chọn m bước lên trên (trong tổng số \(m+n\) bước) có \(C_{m+n}^m\) cách
Còn lại n bước, chọn n cách sang phải, có \(C_n^n\) cách
Vậy tổng cộng có: \(C_{m+n}^m.C_n^n=C_{m+n}^n\) cách