Ai giúp em làm câu 33 với ạ :(((
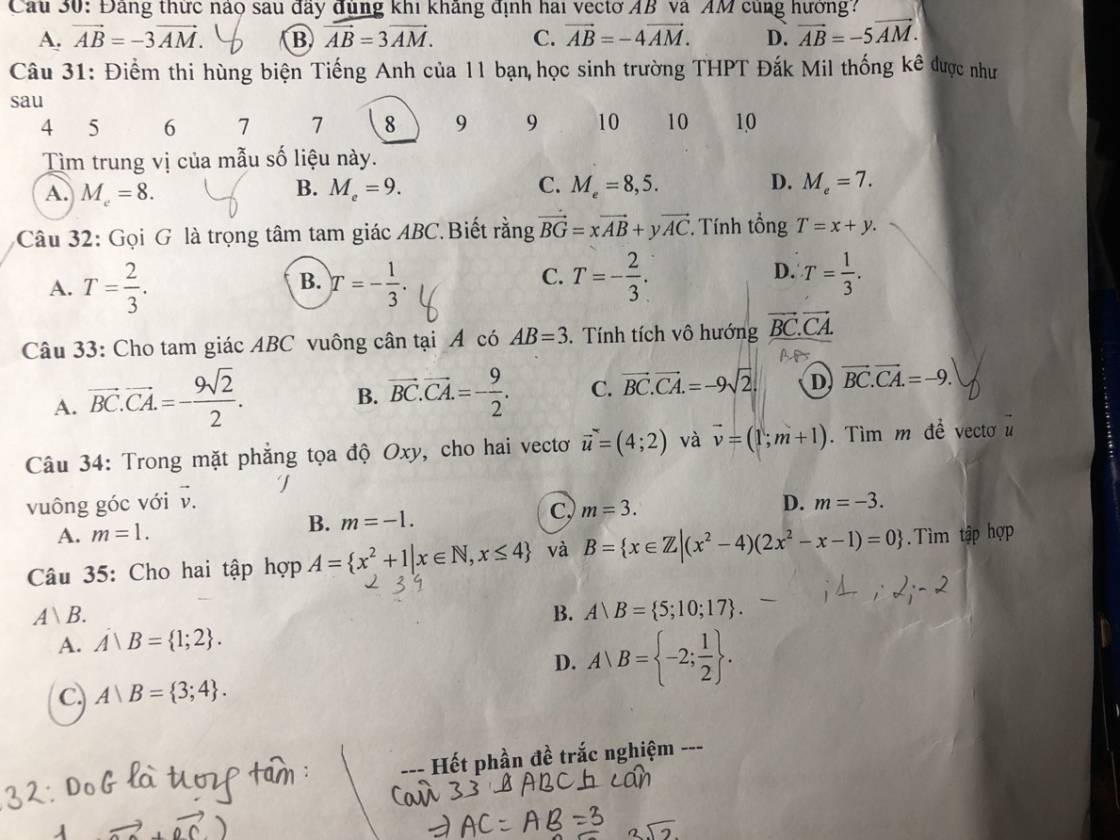
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Cho em xin đề toan hình 1 tiết lớp 7 với ạ !! Em cần gấp !!!!!!! Mọi người giúp em !! Rồi giải câu đó ra cho em luôn ạ !! EM cảm ơn nhiều <3
Câu 1:(1,5 điểm)
Trong hình sau, cho a // b tính 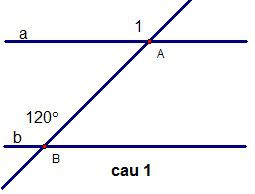
Câu 2:(1,5 điểm)
Cho đoạn thẳng AB dài 3cm. Vẽ đường trung trực của đoạn thẳng AB.
Câu 3:(3 điểm)
Cho a // b; c a.
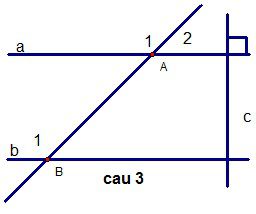
Đường thẳng c có vuông góc với đường thẳng b không ? vì sao?
Cho . tính
,
Câu 4:(4 điểm)
Hình vẽ sau đây cho biết : a // b, ,
.
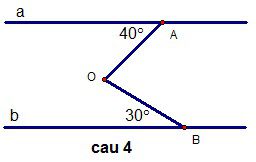
Tính .

a.
Ta có \(BD||AC\) (cùng vuông góc AB)
Áp dụng định lý Talet trong tam giác ACE: \(\dfrac{BE}{BA}=\dfrac{DE}{DC}\)
b.
Ta có \(IK||BD||AC\) \(\Rightarrow EI||AC\)
Áp dụng Talet: \(\dfrac{DC}{ED}=\dfrac{DA}{ID}\Rightarrow\dfrac{DC}{DC+ED}=\dfrac{DA}{DA+ID}\Rightarrow\dfrac{DC}{CE}=\dfrac{DA}{AI}\) (1)
Do \(BD||EK\), áp dụng Talet trong tam giác CEK: \(\dfrac{BD}{EK}=\dfrac{CD}{CE}\) (2)
Do \(BD||EI\), áp dụng Talet trong tam giác AEI: \(\dfrac{BD}{EI}=\dfrac{AD}{AI}\) (3)
Từ(1);(2);(3) \(\Rightarrow\dfrac{BD}{EK}=\dfrac{BD}{EI}\Rightarrow EK=EI\)

Câu 7:
a, \(Fe+H_2SO_4\rightarrow FeSO_4+H_2\)
\(CuO+H_2SO_4\rightarrow CuSO_4+H_2O\)
b, \(n_{H_2}=\dfrac{2,24}{22,4}=0,1\left(mol\right)\)
Theo PT: \(n_{Fe}=n_{H_2}=0,1\left(mol\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\%m_{Fe}=\dfrac{0,1.56}{10}.100\%=56\%\\\%m_{CuO}=44\%\end{matrix}\right.\)
c, \(n_{CuO}=\dfrac{10-0,1.56}{80}=0,055\left(mol\right)\)
Theo PT: \(n_{H_2SO_4}=n_{Fe}+n_{CuO}=0,155\left(mol\right)\)
\(\Rightarrow C\%_{H_2SO_4}=\dfrac{0,155.98}{100}.100\%=15,19\%\)
d, Theo PT: \(\left\{{}\begin{matrix}n_{FeSO_4}=n_{Fe}=0,1\left(mol\right)\\n_{CuSO_4}=n_{CuO}=0,055\left(mol\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}m_{FeSO_4}=0,1.152=15,2\left(g\right)\\m_{CuSO_4}=0,055.160=8,8\left(g\right)\end{matrix}\right.\)
Câu 8:
a, \(CuCO_3+2HCl\rightarrow CuCl_2+CO_2+H_2O\)
b, \(n_{CO_2}=\dfrac{3,36}{22,4}=0,15\left(mol\right)\)
Theo PT: \(n_{CuCO_3}=n_{CO_2}=0,15\left(mol\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\%m_{CuCO_3}=\dfrac{0,15.124}{20}.100\%=93\%\\\%m_{CuCl_2}=7\%\end{matrix}\right.\)
c, \(n_{HCl}=2n_{CO_2}=0,3\left(mol\right)\)
\(\Rightarrow C_{M_{HCl}}=\dfrac{0,3}{0,2}=1,5\left(M\right)\)

Bài 2 : (1) liên kết ; (2) electron ; (3) liên kết ; (4) : electron ; (5) sắp xếp electron
Bài 4 :
$\dfrac{M_X}{4} = \dfrac{M_K}{3} \Rightarrow M_X = 52$
Vậy X là crom,KHHH : Cr
Bài 5 :
$M_X = 3,5M_O = 3,5.16 = 56$ đvC
Tên : Sắt
KHHH : Fe
Bài 9 :
$M_Z = \dfrac{5,312.10^{-23}}{1,66.10^{-24}} = 32(đvC)$
Vậy Z là lưu huỳnh, KHHH : S
Bài 10 :
a) $PTK = 22M_{H_2} = 22.2 = 44(đvC)$
b) $M_{hợp\ chất} = X + 16.2 = 44 \Rightarrow X = 12$
Vậy X là cacbon, KHHH : C
Bài 11 :
a) $PTK = 32.5 = 160(đvC)$
b) $M_{hợp\ chất} = 2A + 16.3 = 160 \Rightarrow A = 56$
Vậy A là sắt
c) $\%Fe = \dfrac{56.2}{160}.100\% = 70\%$


Bài 3:
\(a,\) Gọi \(\left(d\right):y=ax+b\) là đt cần tìm
\(\Leftrightarrow\left\{{}\begin{matrix}a=2\\0a+b=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=2\\b=1\end{matrix}\right.\Leftrightarrow\left(d\right):y=2x+1\)
\(b,\) PT hoành độ giao điểm:
\(-x^2=2x+1\Leftrightarrow\left(x+1\right)^2=0\Leftrightarrow x=-1\Leftrightarrow y=-1\Leftrightarrow A\left(-1;-1\right)\)
Vậy \(A\left(-1;-1\right)\) là tọa độ giao điểm (P) và (d)
Bài 4:
PT có 2 nghiệm \(\Leftrightarrow\Delta'=16-3m\ge0\Leftrightarrow m\le\dfrac{16}{3}\)
Áp dụng Viét: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{8}{3}\\x_1x_2=\dfrac{m}{3}\end{matrix}\right.\)
Mà \(x_1^2+x_2^2=\dfrac{82}{9}\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=\dfrac{82}{9}\)
\(\Leftrightarrow\dfrac{64}{9}-\dfrac{2m}{3}=\dfrac{82}{9}\\ \Leftrightarrow\dfrac{2m}{3}=-2\Leftrightarrow m=-3\left(tm\right)\)

\(b,\Leftrightarrow\left\{{}\begin{matrix}m+1=3\\m-3\ne-3\end{matrix}\right.\Leftrightarrow m=2\\ c,\text{PT giao Ox tại hoành độ 3: }\\ x=-3;y=0\Leftrightarrow\left(m+1\right)\left(-3\right)+m-3=0\\ \Leftrightarrow-2m-6=0\Leftrightarrow m=-3\)

a.
ĐKXĐ: \(\left[{}\begin{matrix}x\ge-1+\sqrt{2}\\x\le-1-\sqrt{2}\end{matrix}\right.\)
\(x^2-2x-1+2\left(x-1\right)\sqrt{x^2+2x-1}=0\)
\(\Leftrightarrow\left(x^2+2x-1\right)+2\left(x-1\right)\sqrt{x^2+2x-1}-4x=0\)
\(\Delta'=\left(x-1\right)^2+4x=\left(x+1\right)^2\)
\(\Rightarrow\left[{}\begin{matrix}\sqrt{x^2+2x-1}=1-x+x+1\\\sqrt{x^2+2x-1}=1-x-x-1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x^2+2x-1}=2\\\sqrt{x^2+2x-1}=-2x\left(x\le0\right)\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x^2+2x-1=4\\x^2+2x-1=4x^2\left(vô-nghiệm\right)\end{matrix}\right.\)
\(\Rightarrow x\)
b.
ĐKXĐ: \(x\ge-\sqrt[3]{3}\)
\(x^3+3-\left(5x-1\right)\sqrt{x^3+3}+6x^2-2x=0\)
Đặt \(\sqrt{x^3+3}=t\ge0\)
\(\Rightarrow t^2-\left(5x-1\right)t+6x^2-2x=0\)
\(\Delta=\left(5x-1\right)^2-4\left(6x^2-2x\right)=\left(x-1\right)^2\)
\(\Rightarrow\left[{}\begin{matrix}t=\dfrac{5x-1-x+1}{2}=2x\\t=\dfrac{5x-1+x-1}{2}=3x-1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x^3+3}=2x\left(x\ge0\right)\\\sqrt{x^3+3}=3x-1\left(x\ge\dfrac{1}{3}\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x^3+2=4x^2\left(x\ge0\right)\\x^3+3=9x^2-6x+1\left(x\ge\dfrac{1}{3}\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left(x-1\right)\left(x^2-3x-3\right)=0\left(x\ge0\right)\\\left(x-1\right)\left(x^2-8x-2\right)=0\left(x\ge\dfrac{1}{3}\right)\end{matrix}\right.\)
\(\Leftrightarrow...\)

Ta có \(\dfrac{1}{2^2}< \dfrac{1}{1.2};\dfrac{1}{3^2}< \dfrac{1}{2.3};...;\dfrac{1}{2022^2}< \dfrac{1}{2021.2022}\)
cộng vế với vế
\(\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{2022^2}< 1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{2021}-\dfrac{1}{2022}\)
\(=1-\dfrac{1}{2022}=\dfrac{2021}{2022}\)
Vậy ta có đpcm
Câu 33:
Vì ΔABC vuông cân tại A nên \(\widehat{B}=\widehat{C}=45^0\)
ΔABC vuông cân tại A
=>\(BC=AB\cdot\sqrt{2}=3\sqrt{2}\)
\(\overrightarrow{BC}\cdot\overrightarrow{CA}=-\overrightarrow{CB}\cdot\overrightarrow{CA}\)
\(=-CB\cdot CA\cdot cos\left(\overrightarrow{CB};\overrightarrow{CA}\right)\)
\(=-3\cdot3\sqrt{2}\cdot cos45\)
\(=-9\sqrt{2}\cdot\dfrac{\sqrt{2}}{2}=-9\)
=>Chọn D