Cho tứ diện đều ABCD cạnh a, G là trọng tâm tam giác BDC. Mặt phẳng qua A, G và song song với BC cắt DB và DC lần lượt tại M và N. Tính diện tích tam giác AMN
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn D.
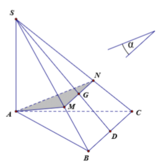
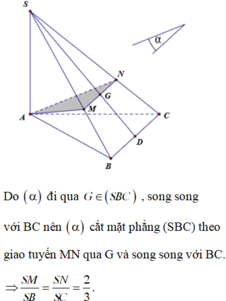
Do ( α ) đi qua G ∈ (SBC), song song với BC nên ( α ) cắt mặt phẳng (SBC) theo giao tuyến MN qua G và song song với BC.
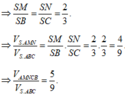
Do tam giác ABC vuông cân tại B, AC = a
2
nên ![]()
Do SA
⊥
(ABC) nên ![]()
![]()

Đáp án B
V S A I J V S A B C = S I S B . S J S C = 2 3 . 2 3 = 4 9 .
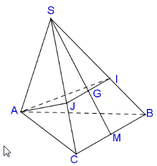

Đáp án D
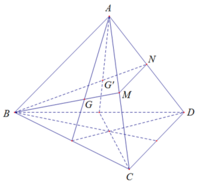
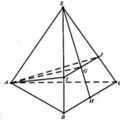
Trong(ABC), ta có: BG cắt AC tại M
Trong (ABD), ta có: BG’ cắt AD tại N
⇒ (BGG’) ∩ (ACD) = MN
Thiết diện cần tìm là (BMN)
Xét tam giác BMN có:
MN = 1 2 CD = a 2 ( MN là đường trung bình của tam giác ACD)
BM = BN = a 3 2 (BM, BN lần lượt là đường trung tuyến của tam giác ABC, ABD)
Áp dụng công thức heron:
S = p p - a p - b p - c = a 2 11 6

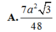
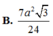
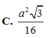
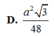

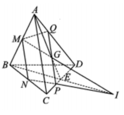


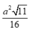
ABCD là tứ diện đều \(\Rightarrow AG\perp\left(BCD\right)\Rightarrow AG\perp DG\)
Gọi E là trung điểm BC, do G là trọng tâm BCD nên theo tính chất trọng tâm
\(\dfrac{DG}{DE}=\dfrac{2}{3}\)
Qua G kẻ đường thẳng song song BC cắt BD và CD tại M và N
Ta có: \(DE=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều) \(\Rightarrow DG=\dfrac{2}{3}DE=\dfrac{a\sqrt{3}}{3}\)
Pitago tam giác vuông ADG: \(AG=\sqrt{AD^2-DG^2}=\sqrt{a^2-\left(\dfrac{a\sqrt{3}}{3}\right)^2}=\dfrac{a\sqrt{6}}{3}\)
Định lý talet: \(\dfrac{GN}{CE}=\dfrac{DG}{DE}=\dfrac{2}{3}\Rightarrow GN=\dfrac{2}{3}CE=\dfrac{2}{3}.\dfrac{a}{2}=\dfrac{a}{3}\)
\(\Rightarrow MN=2GN=\dfrac{2a}{3}\)
\(S_{AMN}=\dfrac{1}{2}AG.MN=\dfrac{a^2\sqrt{6}}{9}\)