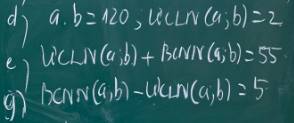
bài này cóa ai giúp tui hưm ạ, cần giúp gấp í, thanks rấc nhiều
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
21 tháng 1
p: \(\left(-\dfrac{2}{5}\right)^2+\dfrac{17}{-18}\cdot\dfrac{36}{34}-\left(-\dfrac{2}{3}\right)^3\)
\(=\dfrac{4}{25}-\dfrac{17}{34}\cdot\dfrac{36}{18}-\dfrac{-8}{27}\)
\(=\dfrac{4}{25}+\dfrac{8}{27}-1=\dfrac{-367}{675}\)
q: \(\left(-\dfrac{1}{2}\right)^0-\dfrac{-1}{3}\cdot\dfrac{-9}{12}+\dfrac{2^4}{-4}\)
\(=1-\dfrac{1}{3}\cdot\dfrac{3}{4}+\dfrac{16}{-4}\)
\(=1-\dfrac{1}{4}-4=-3-\dfrac{1}{4}=-\dfrac{13}{4}\)
r: \(\left(-5\right)\cdot\dfrac{17}{45}-\left(-\dfrac{2}{3}\right)^2+\left(-\dfrac{20}{2023}\right)^0\)
\(=-\dfrac{17}{9}-\dfrac{4}{9}+1\)
\(=-\dfrac{21}{9}+1=-\dfrac{12}{9}=-\dfrac{4}{3}\)
NT
1
29 tháng 12 2023
Bài 19:
Chu vi hình vuông là: \(\left(12+6\right)\cdot2=36\left(cm\right)\)
Độ dài cạnh hình vuông là 36/4=9(cm)
Diện tích hình vuông là \(9^2=81\left(cm^2\right)\)
Bài 20:
Độ dài đường cao là \(\dfrac{160}{4}=40\left(m\right)\)
Diện tích miếng đất là: \(60\cdot40=2400\left(m^2\right)=0,24\left(ha\right)\)
Khối lượng ngô thu hoạch được là:
\(0,24:3\cdot13,5=1,08\left(tấn\right)=1080\left(kg\right)\)
QT
2
H9
HT.Phong (9A5)
CTVHS
6 tháng 7 2023
Bài 2:
a) \(\dfrac{2}{15}-\dfrac{7}{10}=\dfrac{4}{30}-\dfrac{21}{30}=-\dfrac{17}{30}\)
b) \(\dfrac{-3}{14}+\dfrac{2}{21}=\dfrac{-9}{42}+\dfrac{4}{42}=\dfrac{-5}{42}\)
c) \(\dfrac{-6}{9}+\dfrac{-12}{16}=\dfrac{-96}{144}+\dfrac{-108}{144}=\dfrac{-204}{144}=-\dfrac{17}{12}\)
H9
HT.Phong (9A5)
CTVHS
6 tháng 7 2023
Bài 3:
a) \(\dfrac{3}{8}+\dfrac{-5}{6}=\dfrac{3}{8}-\dfrac{5}{6}=\dfrac{18}{48}-\dfrac{40}{48}=-\dfrac{22}{48}=-\dfrac{11}{24}\)
b) \(\dfrac{-8}{18}-\dfrac{15}{27}=\dfrac{-24}{54}-\dfrac{30}{54}=\dfrac{-54}{54}=-1\)
c) \(\dfrac{2}{21}-\dfrac{-1}{28}=\dfrac{8}{84}-\dfrac{-3}{84}=\dfrac{11}{84}\)
4 tháng 11 2023
Người thứ 3 gieo được \(3\cdot3=3^2\left(hạt\right)\)
Người thứ 4 gieo được \(3^2\cdot3=3^3\left(hạt\right)\)
...
Người thứ 102 gieo được: \(3^{100}\cdot3=3^{101}\left(hạt\right)\)
Tổng số hạt gieo được là:
\(A=3^0+3+3^2+...+3^{101}\)
\(=\left(1+3+3^2\right)+...+\left(3^{99}+3^{100}+3^{101}\right)\)
\(=13+3^3\cdot13+...+3^{99}\left(1+3+3^2\right)\)
\(=13\cdot\left(1+3^3+...+3^{99}\right)⋮13\)
21 tháng 10 2021
Bài 6:
a) \(x^2-2x+4=\left(x^2-2x+1\right)+3=\left(x-1\right)^2+3>0\forall x\)
b) \(-x^2+4x-5=-\left(x^2-4x+4\right)-1=-\left(x-2\right)^2-1< 0\forall x\)
c) \(\left(x-2\right)\left(x-4\right)+3=x^2-6x+11=\left(x^2-6x+9\right)+2=\left(x-3\right)^2+2>0\forall x\)
d) \(-2x^2+5x-19=\dfrac{-4x^2+10x-38}{2}=\dfrac{-\left(4x^2-10x+6,25\right)-31,75}{2}=\dfrac{-\left(2x-2,5\right)^2-31,75}{2}< 0\forall x\)
21 tháng 10 2021
Câu 5:
\(a^3+b^3=3ab-1\\ \Leftrightarrow\left(a+b\right)^3-3ab\left(a+b\right)-3ab+1=0\\ \Leftrightarrow\left(a+b+1\right)\left(a^2+2ab+b^2-a-b+1\right)-3ab\left(a+b+1\right)=0\\ \Leftrightarrow\left(a+b+1\right)\left(a^2+b^2+1-ab-a-b\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}a+b+1=0\left(vô.lí.do.a,b>0\right)\\a^2+b^2+1-ab-a-b=0\left(1\right)\end{matrix}\right.\\ \left(1\right)\Leftrightarrow2a^2+2b^2+2-2ab-2a-2b=0\\ \Leftrightarrow\left(a-b\right)^2+\left(a-1\right)^2+\left(b-1\right)^2=0\\ \Leftrightarrow\left\{{}\begin{matrix}a-b=0\\a-1=0\\b-1=0\end{matrix}\right.\Leftrightarrow a=b=1\)
Vậy \(T=\left(1-2\right)^{2020}+\left(1-1\right)^{2021}=\left(-1\right)^{2020}+0=1\)
với ạ cần gấp ngày mai
NV
Nguyễn Việt Lâm
Giáo viên
28 tháng 3 2021
\(=\lim\left(\sqrt[3]{n^3-2n}\left(\sqrt[]{n^2+n}-n\right)+n\sqrt[3]{n^3-2n}-n^2\right)\)
\(=\lim\left(\dfrac{n\sqrt[3]{n^3-2n}}{\sqrt[]{n^2+n}+n}-\dfrac{2n^2}{\sqrt[3]{\left(n^3-2n\right)^2}+n\sqrt[3]{n^3-2n}+n^2}\right)\)
\(=\lim\left(\dfrac{n\sqrt[3]{1-\dfrac{2}{n^2}}}{\sqrt[]{1+\dfrac{1}{n}}+1}-\dfrac{2}{\sqrt[3]{\left(1-\dfrac{2}{n^2}\right)^2}+\sqrt[3]{1-\dfrac{2}{n^2}}+1}\right)\)
\(=+\infty-\dfrac{2}{3}=+\infty\)
17 tháng 4 2022
\(\left|2x-3\right|=3-2x\)
\(ĐK:x\le\dfrac{3}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=3-2x\\3-2x=3-2x\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\0=0\left(đúng\right)\end{matrix}\right.\)
Vậy \(S=\left\{x\in R;x=\dfrac{3}{2}\right\}\)
A
1
d: Ta có: ƯCLN(a,b)=2
=>\(\left\{{}\begin{matrix}a=2x\\b=2y\end{matrix}\right.\)
\(a\cdot b=120\)
=>\(2x\cdot2y=120\)
=>\(x\cdot y=30\)
mà x,y là các số nguyên dương
nên \(\left(x,y\right)\in\left\{\left(1;30\right);\left(2;15\right);\left(3;10\right);\left(5;6\right);\left(6;5\right);\left(10;3\right);\left(15;2\right);\left(30;1\right)\right\}\)
=>\(\left(a,b\right)\in\left\{\left(2;60\right);\left(4;30\right);\left(6;20\right);\left(10;12\right);\left(12;10\right);\left(20;6\right);\left(30;4\right);\left(60;2\right)\right\}\)